Solving Linear Equations in One Variable
Abstract
Elementary Algebra: An introduction to solving linear equations in one variable.
1 Module Overview
Learning how to solve various algebraic equations is one of our main goals in
algebra. This module introduces
the basic techniques for solving linear equations in one variable.
(Prerequisites: Working knowledge of real
numbers and their operations.)
Objectives
• Define Linear Equations in One Variable
• Solutions to Linear Equations
• Solving Linear Equations
• Combining Like Terms and Simplifying
• Literal Equations
2 Define Linear Equations in One Variable
We begin by establishing some definitions.
Definition 1: Equation
An equation is a statement indicating that two algebraic expressions are equal.
Definition 2: Linear Equation in One Variable
A linear equation in one variable x is an equation that can be written in the
form ax +b = 0 where
a and b are real numbers and a ≠ 0.
Following are some examples of linear equations in one variable, all of which
will be solved in the course
of this module.


3 Solutions to Linear Equations in One Variable
The variable in the linear equation 2x + 3 = 13 is x. Values that can replace
the variable to make a true
statement compose the solution set. Linear equations have at most one solution.
After some thought, you
might deduce that x = 5 is a solution to 2x + 3 = 13. To verify this we
substitute the value 5 in for x and
see that we get a true statement, 2 (5) + 3 = 10 + 3 = 13.
Example 1
Is x = 3 a solution to -2x - 3 = -9?
Yes, because -2 (3) - 3 = -6 - 3 = -9
Example 2
Is 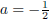 a solution to -10a + 5 = 25?
a solution to -10a + 5 = 25?
No, because 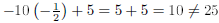
When evaluating expressions, it is a good practice to replace all variables with
parenthesis first , then sub-
stitute in the appropriate values. By making use of parenthesis we could avoid
some common errors using
the order of operations .
Example 3
Is y = -3 a solution to 2y - 5 = -y - 14 ?
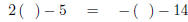 |
Replace variables with parenthesis. |
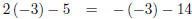 |
Substitute the appropriate value. |
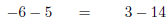 |
Simplify. |
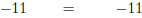 |
True. |
Yes because y = -3 produces a true mathematical statement .
4 Solving Linear Equations in One Variable
When the coefficients of linear equations are numbers other than nice easy
integers, guessing at solutions
becomes an unreasonable prospect. We begin to develop an algebraic technique for
solving by first looking
at the properties of equality .
4.1 Properties of Equality
Given algebraic expressions A and B where c is a real number:
Property 1: Addition Property of Equality
If A = B then A + c = B + c
Property 2: Subtraction Property of Equality
If A = B then A - c = B - c
Property 3: Multiplication Property of Equality|
If A = B and c ≠ 0 then cA = cB
Property 4: Division Property of Equality
If A = B and c ≠ 0 then 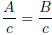
Note: Multiplying or dividing both sides of an equation by zero is carefully
avoided. Dividing
by zero is undefined and multiplying both sides by zero will result in an
equation 0=0.
To summarize , the equality is retained if we add, subtract, multiply and divide
both sides of an equation
by any nonzero real number. The central technique for solving linear equations
involves applying these
properties in order to isolate the variable on one side of the equation.
Example 4
Use the properties of equality to solve: x + 3 = -5
| x + 3 = -5 | |
| x + 3 - 3 = -5 - 3 | Subtract 3 on both sides. |
| x = -8 | Simplify |
The solution set is 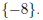
Example 5
Use the properties of equality to solve: -5x = -35
| -5x = -35 | |
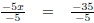 |
Divide both sides by -5. |
| x = 7 | Simplify |
The solution set is 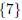 .
.
Two other important properties are:
Property 5: Symmetric Property
If A = B then B = A.
Property 6: Transitive Property
If A = B and B = C then A = C.
When solving, we often see 2 = x but that is equivalent to x = 2.
4.2 Isolating the Variable
The idea behind solving in algebra is to isolate the variable. If given a linear
equation of the form ax+ b = c
then we can solve it in two steps. First use the equality property of addition
or subtraction to isolate the
variable term. Next isolate the variable by using the equality property of
multiplication or division. The
property choice depends on the given operation, we choose to apply the opposite
property of the given
operation. For example, if given a term plus three we would first choose to
subtract three on both sides of
the equation. If given two times the variable then we would choose to divide
both sides by two.
Example 6
Solve 2x + 3 = 13 .
| 2x + 3 = 13 | |
| 2x + 3 - 3 = 13 - 3 | Subtract 3 on both sides. |
| 2x = 10 | |
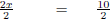 |
Divide both sides by 2. |
| x = 5 |
The solution set is 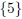 .
.
Example 7
Solve -3x - 2 = 9 .
| -3x - 2 = 9 | |
| -3x - 2 + 2 = 9 + 2 | Add 2 to both sides. |
| -3x = 11 | |
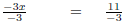 |
Divide both sides by -3. |
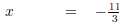 |
The solution set is 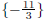 .
.
Example 8
Solve 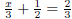 .
.
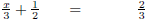 |
|
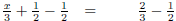 |
Subtract 1/2 on both sides. |
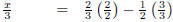 |
|
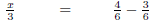 |
|
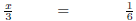 |
|
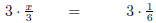 |
Multiply both sides by 3. |
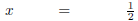 |
The solution set is 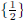
In order to retain the equality, we must perform the same operation on both
sides of the equation. To isolate
the variable we want to remember to choose the opposite operation not the
opposite number. For example,
if we have -5x = 20 then we choose to divide both sides by -5, not 5.
Figure 1: Video Example 01
4.2.1 Multiplying by the Reciprocal
Recall that when multiplying reciprocals the result is 1, for example,
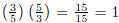 . We can use this
. We can use this
fact when the coefficient of the variable is a fraction.
Example 9
Solve 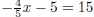
 |
|
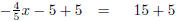 |
Add 5 on both sides. |
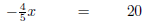 |
|
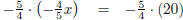 |
Multiply both sides by - 5/4 . |
| 1x = -5 · 5 | Simplify. |
| x = -25 |
The solution set is 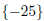
| Prev | Next |