Solving Quadratic Equations by F
Solving Quadratic Equations by Factoring
A quadratic equation (also called a “second- degree
polynomial ”) is an equation that can be
written as ax2 + bx + c = 0
Solve the equation
| Step … | Then … |
| x2 + 3x + 2 = 0 | Factor the equation |
| (x + 2)(x + 1) = 0 | Set each factor equal to 0 to get two equations . |
| x + 2 = 0 and x + 1 = 0. | Solve each equation to get two solutions. |
| x = -2 and x = -1 | These are the two solutions to the equation . |
Then check the solutions. First we’ll do x = -2.
(-2)2 + 3(-2) + 2 = 4 - 6 + 2 = 0. Good. Check the other solution, x
= -1
(-1)2 + 3(-1) + 2 = 1 - 3 + 2 = 0. Good. Both solutions check
Comments:
1. It is fine to write: x = -1, -2 or x = -2, -1. It is not OK to write x = (-1,
-2). Those brackets
denote the coordinates of a single point. What we have here are two values for x
that solve the
equation. If you must be fancy you can use set notation x = {-1, -2}
2. Quadratic equations usually have two solutions. (See below for exceptions).
3. The procedure here is quite different from solving equations that don’t have
a squared term in
them. To solve the equation 2x + 5 = 9, the procedure is get x alone on one side
of the equation.
This does not work to solve a quadratic equation.
Why does it work? The basic idea is the “zero-factor property,” which
says, “If two numbers
multiply to zero , then one of them must be zero.” That is, if a·b = 0, then
either a = 0 or b = 0.
You can’t multiply two non- zero numbers and get zero.
The point of factoring the quadratic equation is to produce something that looks
like a ·b = 0 so
that we can solve the simple a = 0 and b = 0 equations.
Another example.
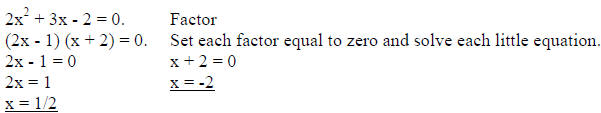
The solutions are x = ½, -2
Check:
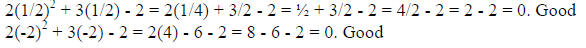
SPECIAL CASES
1. A perfect square equation has only one solution.
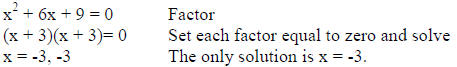
2. The difference of squares .
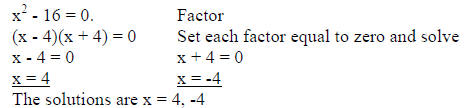
PROBLEMS

GRAPHING QUADRATIC EQUATIONS
1. Graph y = x2. Let’s pick values for x and find y for each x.
The figure shown is what results from
plotting the points . The curve is called a
parabola .
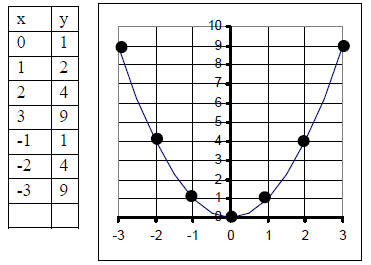
2. Graph y = x2 + 1
Notice that this is just the graph y = x2 moved up
by 1.
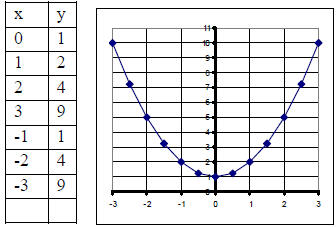
3. Graph y = x2 - 2
4. Graph y = - x2
5.
6.
| Prev | Next |