SOLVING RATIONAL EQUATIONS
Recall that when solving for fractions that are added
or subtracted from each
other that a common denominator must be found. This is true even if the
denominator contains a variable. An extra condition that must always be
considered is that any value of the variable that makes the denominator zero
must be excluded.
Example 1. Solve
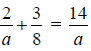
Step 1. Find the LCD.
The LCD for this problem is 8a. Also a ≠ 0 .
Step 2. Multiply all terms by the LCD .
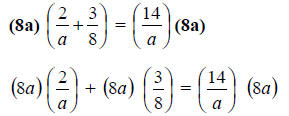
Step 3. Simplify .
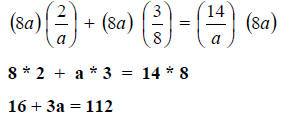
Step 4. Solve for a.
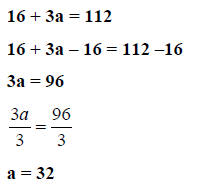
This is the solution since a ≠ 0 and 32 yields a valid check.
Example 2. Solve
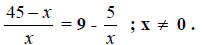
Step 1. Find the LCD.
The LCD for this problem is x .
Step 2. Multiply all terms by the LCD of x.
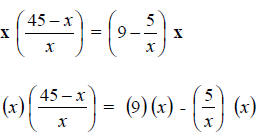
Step 3. Simplify.
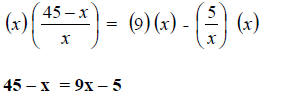
Step 4. Solve for x.
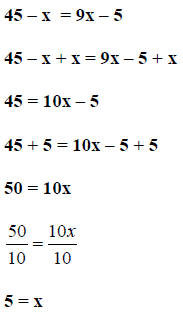
This is the solution since x ≠ 0 and 5 yields a valid check.
Example 3. Solve
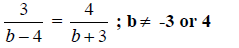
Step 1. Find the LCD.
The LCD for this problem is ( b – 4 ) ( b + 3 ).
Step 2. Multiply all terms by the LCD.
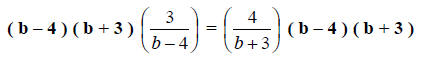
Step 3. Simplify.
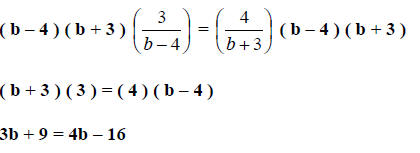
Step 4. Solve for b.
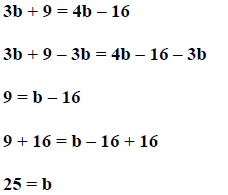
This is the solution since b ≠ -3 or 4 and 25 yields a valid check.
Example 4. Solve
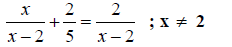
Step 1. Find the LCD.
The LCD for this problem is 5 ( x - 2 ).
Step 2. Multiply all terms by the LCD.
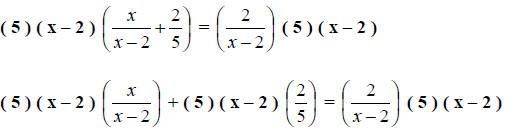
Step 3. Simplify
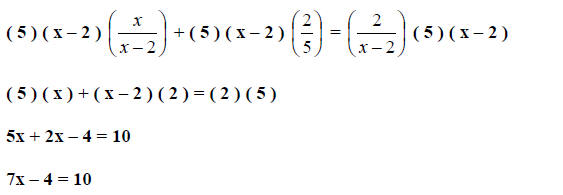
Step 4. Solve for x.
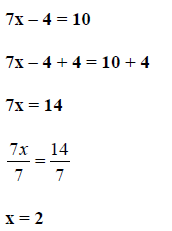
This is not the solution since 2 was excluded at the
beginning of the problem.
This problem then has no real solutions .
Where two numbers are compared using division , a ratio
is said to exist.
When two ratios are made equal to each other a proportion exists . These
ideas lead to the cross-multiplication property of proportions , which states:
If 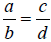 ( b ≠ 0 and d ≠
0 ) then ad = bc
( b ≠ 0 and d ≠
0 ) then ad = bc
Example 5. Using cross-multiplication, solve
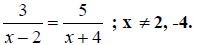
Step 1. Apply the property to the problem.
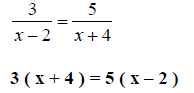
Step 2. Simplify.
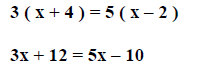
Step 3. Solve for x.
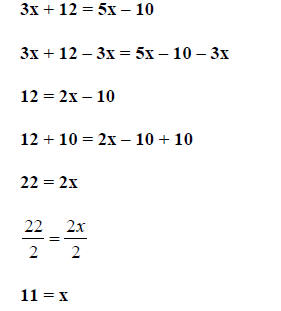
This is the solution since x ≠ 2 or -4 and 11 yields a valid check.
| Prev | Next |