Elementary Algebra Review

EQUATIONS AND INEQUALITIES

Simplifying Algebraic Expressions

Simplifying generally means creating equivalent expressions that contain fewer additions and or
multiplications. To simplify algebraic expressions, combine like terms by adding their coefficients and
keeping the variable parts the same. To simplify expressions containing parentheses, remove all
parentheses and combine like terms . Remember to work problems containing parentheses from the inner
most set outward.

Example:		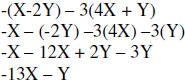Distribute constants and signs
		Perform all multiplications
		Group like terms

Solving Linear Equations

The solution to an equation is a number that, when substituted into the equation for the variable, results in
a true equation. Solving the equation means finding all such numbers. The general method of solving an
equation is to replace the given equation with simpler and simpler equations until an equation of the form
variable=constant occurs. The constant is then called the solution of the equation.

The two properties that are used to form these simpler equations are The Additive Property of Equations
and The Multiplicative Property of Equations.

The Additive Property of Equations : Adding (or subtracting) the same quantity to both sides of an
equation will not change the solution set of the equation.

Example 1: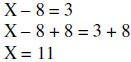
		Add 8 to both sides

The Multiplicative Property of Equations: Multiplying (or dividing) both sides of an equation by the same
nonzero number will not change the solution set of the equation.

Example 2:	5X = 27
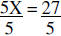		Divide both sides by 5

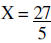Anytime more than one property is used, always use the addition property before the multiplication
property.

Example 3:

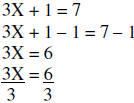
Solving Inequalities

An inequality states that one quantity is larger than another. The solution set of an inequality is the set of
all numbers that make the inequality true when substituted into the original inequality. These solution
sets are found using similar properties as those used to solve equations.

Example: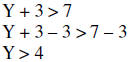
		Subtract 3 from both sides
		Graph the solution set

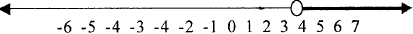
The Multiplicative Property of Inequalities: Multiplying (or dividing) both sides of an inequality by the
same positive non -zero number will not change the solution set of the inequality. Multiplying (or
dividing) both sides of an inequality by the same non-zero negative number reversing the inequality does
not change the solution set of the inequality.

Example 2: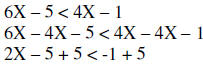
		Subtract 4X
		Add 5
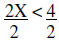		Divide by positive 2

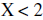Example 3: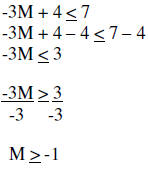
		Subtract 4

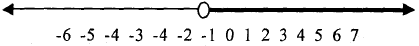
Exercises
Simplify each of the following

1. -3V + 7V – V

2. 12X – 3Y + 5X + 5Y

3. -7M + 9(2M – 3)

4. –(2X – 7Y) – 3(2Y – 11X)

5. 3[2X – 3(X – 2Y)] + 3Y

Solve each of the following Equations

11. Solve for X: (3X + Y) – (Y-X) = 5 (2X + Y)

12. The sum of two numbers is 18. The difference between four times the smaller number and seven is
equal to the sum of two times the larger number and five. Find the two numbers.

13. Jane bought a television set at a 20% off sale. If she paid $360 for the set, what was the original price.

14. How many gallons of water must be mixed with 5 gal of 20% salt solution to make a 16% salt
solution?

15. The perimeter of a triangle is 23ft. One side is twice the second side. The third side is 3ft. more than
the second side. Find the measurements of each side.

Solve the following inequalities. Graph your results.

16. 2X < 6X – 8

17. 13 – 4X < X – 2

18. 4X + 9 > X – 7

19. Two sides of a triangle must be 8m and 12m. The perimeter must be at least 24m at most 39m.
Determine the length that can be used for the third side.

20. An insurance company is developing a new policy that is expected to have an average annual claim of
at least $409. The yearly premium for the policy will be $390. To make up the underwriting loss the
company plans to put the premium money into an investment that is expected to yield an annual profit of
between 4.3% and 4.8% after other expenses are covered. Under these conditions, will this policy make
money for the company?

EXPONENTS AND POLYNOMIALS

Integer Exponents

The following properties are used to work with exponents.

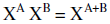	To multiply with the same base you add exponents
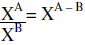	To divide with the same base you subtract exponents
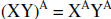	Exponents distribute over multiplication
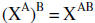	A power to a power is the product of the powers
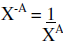	Negative exponents imply reciprocals

Example 1:		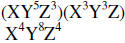Add exponents for like bases
Example 2:		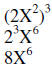Multiple Exponents
Example 3: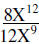
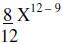		Divide the numerical coefficients Subtracts the exponents on the variables
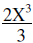		Simplify
Example 4: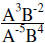
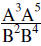		Make all exponents positive
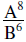		Add exponents for the like bases