Exponential and Logarithmic Functions
Properties of the
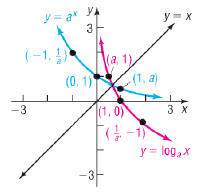
Logarithmic Function
•Properties of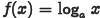 
, a >1
•Domain: Positive real numbers ; (0, ∞)
•Range: All real numbers
•Intercepts:
•x- intercept of x = 1
•No y-intercepts
•y-axis is horizontal asymptote
•Increasing and one-to-one.
•Smooth and continuous
•Contains points (1,0), (a, 1) and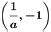 
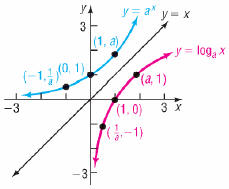
•Properties of 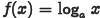, 0 <a
<1
•Domain: Positive real numbers; (0, ∞)
•Range: All real numbers
•Intercepts:
•x-intercept of x= 1
•No y-intercepts
•y-axis is horizontal asymptote
•Decreasing and one-to-one.
•Smooth and continuous
•Contains points (1,0), (a, 1) and
Special Logarithm Functions
•Natural logarithm:
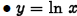if and only if
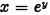
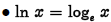
• Common logarithm :
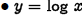if and only if
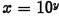
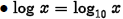
•Example. Graph the function
Problem: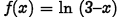 
Answer:
Logarithmic Equations
•Examples. Solve the logarithmic
equations. Give exact answers.
(a) Problem: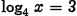
Answer:
(b) Problem: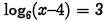 
Answer:
(c) Problem: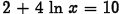 
Answer:
•Examples. Solve the exponential
equations using logarithms . Give
exact answers.
(a) Problem: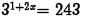
Answer:
(b) Problem: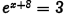 
Answer:
Key Points
•Logarithmic Functions
•Domain and Range of Logarithmic Functions
•Graphing Logarithmic Functions
•Properties of the Logarithmic Function
•Special Logarithm Functions
•Logarithmic Equations
Properties of
Logarithms
Section 4.5
Properties of Logarithms
•Theorem. [Properties of Logarithms]
For a >0, a≠1, and r some real
number:
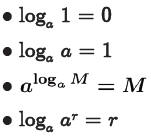
•Theorem. [Properties of Logarithms]
For M, N, a >0, a≠1, and r some
real number:
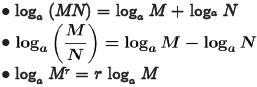
•Examples. Evaluate the following
expressions.
(a) Problem: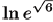
Answer:
(b) Problem: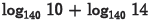 
Answer:
(c) Problem: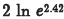 
Answer:
•Examples. Evaluate the following
expressions if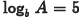 
and
.
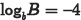(a) Problem: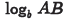
Answer:
(b) Problem: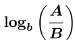 
Answer:
(c) Problem: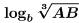
Answer:
•Example. Write the following
expression as a sum of logarithms .
Express all powers as factors .
Problem: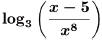
Answer:
•Example. Write the following
expression as a single logarithm.
Problem: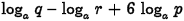 
Answer:
•Theorem. [Properties of Logarithms]
For M, N, a >0, a≠1,
•If M= N, then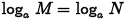 
•If 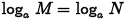, then M= N
•Comes from fact that exponential and
logarithmic functions are inverses.
Logarithms with Bases
Other than e and 10
•Example.
Problem: Approximate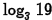 
rounded to
four decimal places
Answer:
•Theorem. [ Change -of- Base Formula ]
If a≠1, b≠1 and Mare all positive
real numbers, then
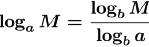
•In particular
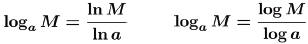
•Examples. Approximate the following
logarithms to four decimal places
(a) Problem: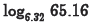
Answer:
(b) Problem: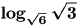 
Answer:
Key Points
•Properties of Logarithms
•Properties of Logarithms
•Logarithms with Bases Other than e
and 10
Logarithmic and
Exponential
Equations
Section 4.6
Solving Logarithmic Equations
•Example.
Problem: Solve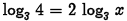
algebraically .
Answer:
•Example.
Problem: Solve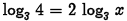
graphically.
Answer:
•Example.
Problem: Solve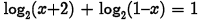 
algebraically.
Answer:
•Example.
Problem: Solve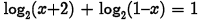
graphically.
Answer:
Solving Exponential Equations
•Example.
Problem: Solve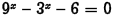 
algebraically.
Answer:
•Example.
Problem: Solve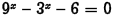
graphically.
Answer:
•Example.
Problem: Solve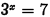 
algebraically. Give
an exact answer, then approximate your
answer to four decimal places.
Answer:
•Example.
Problem: Solve 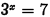graphically.
Approximate your answer to four
decimal places.
Answer:
•Example.
Problem: Solve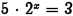 
algebraically.
Give an exact answer, then approximate
your answer to four decimal places.
Answer:
•Example.
Problem: Solve 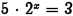graphically.
Approximate your answer to four
decimal places.
Answer:
•Example.
Problem: Solve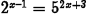 
algebraically.
Give an exact answer, then approximate
your answer to four decimal places.
Answer:
•Example.
Problem: Solve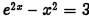 
graphically.
Approximate your answer to four
decimal places.
Answer:
Key Points
•Solving Logarithmic Equations
•Solving Exponential Equations
| Prev | Next |