Factoring polynomials

Two important theorems for real polynomials . To factor a polynomial means to write it as a product
of polynomials of lower degree. A complete factoring means to write a polynomial as a product of polynomials
that cannot be further factored. The following two theorems give us some insight into how this can be done.
The first result connects the four different ideas of algebra together (functions, equations, expressions, and
graphs) for polynomials, while the second one shows the best we can hope for when factoring.

•The Zero Theorem. If p is a polynomial and c is a number (possibly complex), then the following
4 statements are equivalent :

1. p(c) = 0; that is, c is a zero of the function p.
2. x = c is a solution to the equation p (x) = 0.
3. (x - c) can be factored out of the expression p (x).
4. If c is real, then (c, 0) is an x- intercept of the curve y = p(x).

•The Real Factorization theorem. Any polynomial p can be factored uniquely into a product
involving the following

  - The leading coefficient a
  - Linear terms of the form (x - c), where c is a zero of p
  - Quadratic terms of the form (x^2 + ux + v) with no real zeros, called irreducible quadratics.

Complex numbers and factoring completely. If we only use real numbers, then not every polynomial
can be factored into simple linear terms . For example, x^2 + 1 has no real solutions, so it cannot be factored
further. However, if we allow complex numbers -- and in particular, the \imaginary" number
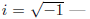
into our factorizations, then x^2 +1 can be factored as (x-i)(x-i). It turns out that this is true in general,
as indicated by the following, penultimate theorems of college algebra.

•The Fundamental Theorem of Algebra. An n-th degree polynomial has exactly n complex zeros,
counting multiplicities (repetitions of the same factor).

•Linear Factorization Theorem. If p is a n-th degree polynomial with complex coefficients, then p
can be factored in the form

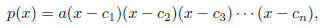
where a is the leading coefficient of p and the numbers 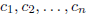are n complex (possibly repeated)
zeros of p.

Moreover, if the coefficients of p are all real numbers, then any non-real roots always occur in pairs of
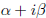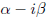the form and , called complex conjugates.

Factoring techniques. There are two main techniques to use in order to factor a long, complicated
polynomial into a product of simpler ones .

•Long division. This is a technique that can be used to divide a polynomial p(x) by any other
polynomial d(x) to get a quotient q(x) and a remainder r(x), so that

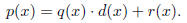
If the remainder is 0, then d(x) is a factor of p(x).
The process of long division is as follows :

1. Set up the division problem by writing out both the divisor d(x) (the polynomial you're dividing
by) and the dividend p(x) (the polynomial you're dividing into) in standard form, with all missing
powers of x included with 0 coefficients.

2. If the degree of the divisor is less than or equal to the degree of the dividend, go to Step 3.
Otherwise, go to step 6.

3. Determine the multiplier monomial required to make the leading term of the divisor to match the
leading term of the dividend. Write this above the vinculum (the long horizontal line on the top
of the division symbol).

4. Multiply the divisor through by this monomial, and write the resulting polynomial underneath
the dividend, lined up by matching powers of x.

5. Subtract the bottom line from the top line (don't forget to distribute the negative through!).
When finished, drop down the next term from p(x). This polynomial is now the new dividend,
go back to Step 2.

6. If the degree of the divisor is greater than the degree of the dividend, then the long division is
complete. The sum of the multiplier monomials above the vinculum is the quotient q(x), and the
final dividend is the remainder r(x).

•The Remainder Theorem. The remainder when p(x) is divided by (x-c) precisely the value p(c).
That is, r = p(c).

•Synthetic division. This is a quick, tabular version of long division that be used to divide a polynomial only by a factor of the form (x - c) for some number c - even complex ones!

The process of synthetic division is as follows:

1. Set up the division problem by writing out the coefficients of p(x) in standard form, with 0s to
mark any missing powers of x, and putting the value c in a box to the left of this. Give yourself
two rows to work with, and draw a line to separate them.

2. Under the leading coefficient of p(x), draw a down arrow in the second row and "drop" the
coefficient down to the third row.

3. Multiply the number in the third row by c, and write the product in next available space in the
second row.

4. Add the numbers in the first and second row together, and write the sum in the third row. Repeat
Steps 3 and 4 until the third row is filled.

5. The last number in the third row is the remainder r, the preceding list of numbers give the
coefficients of the quotient q(x) in standard form.

Finding expressions to factor out. There are three important techniques to help with finding roots to
factor out of a polynomial that don't depend on \dumb luck."

• Using the graph . The x-intercepts of a graph correspond to zeros of the function, and so provide
candidates to be factored out. Use synthetic division to see if they work.

•Educated guesses. Make a guess as to a zero of the polynomial, either blindly or with the help
of a graph, and test it with synthetic division. If you're lucky and find a zero, you'll already have
the factorization done. If you don't, you can use synthetic division to improve your guesses. Some
guidelines.

  - Intermediate values. If the remainder changes sign after two unsuccessful guesses, a true root
must lie between those guesses.
  - Too big a guess. If your guess is positive and the numbers in the bottom row are positive too, the
guess is too big.
  - Too small a guess. If your guess is negative and the numbers in the bottom row alternate sign,
the guess is too small.
  - Guessing fractions. For a polynomial with integer coefficients, the only possible rational roots of
the polynomial take the form

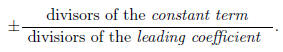
Hence, for a value x = c/d to even possibly be a zero, c must divide a₀ and d must divide a_n. If
both of these don't happen, then it's not worth making the guess.

•Complex roots. This works for any polynomial with real coefficients. Since complex roots always
come in conjugate pairs 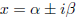, we can get a real factor of p(x), since multiplying

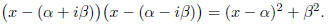
will always be an irreducible quadratic that can be factored out of the polynomial using long division.