Inverse Functions
• Let 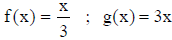
What happens when we compose f and g ?
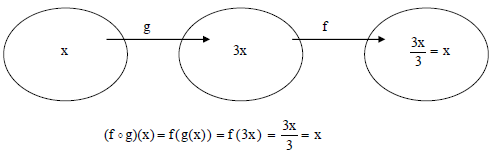
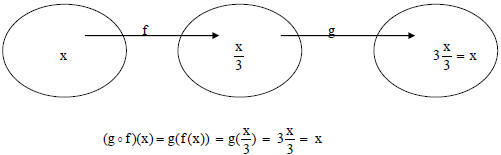
Notice that one function ‘undoes’ the other, producing a
final answer of x in both cases.
We say that f and g are inverses of each other.
• Definition : Two functions f and g are inverses of each other if
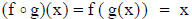
and 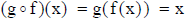
• example : Verify that 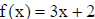 and
and 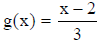 are inverses of each other.
are inverses of each other.
• Notation : The inverse of function f is denoted by
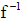
• In the example above, we could write
![]() and
and
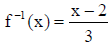
• We can also restate the definition of inverse functions as
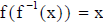 and
and 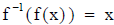
• example : Verify that if 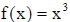 , then
, then
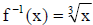
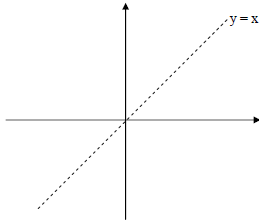
• Result : The graphs of f and
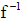 are reflections of each other about the line
y = x.
are reflections of each other about the line
y = x.
• example : Graph the functions f and 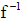 in the
example above.
in the
example above.
• How do we find the inverse of a function?
• The algorithm:
1. Write the equation y = f ( x ) that defines the function.
2. Interchange the variables x and y .
3. Solve for 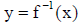
• example : Find the inverse of y = 3x + 2
1. y = 3x + 2
2. x = 3y + 2 ( interchange x and y )
3. 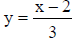 ( solve for
( solve for 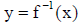 )
)
So,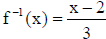
• example : Find the inverse of f (x) = 4 − 2x
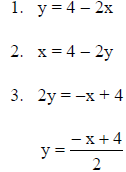
so,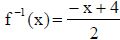
• Does every function have an inverse function?
• To answer this question, think about the fact that the
graphs of f and ![]() are reflections of each
are reflections of each
other about the line y = x.
• Horizontal Line Test : A function has an inverse if no
horizontal straight line intersects its graph
more than once. The function is said to be one-to-one.
• example : Does y = x2 have an inverse?
• example : Does y = x2 , x ≥ 0 have an inverse?
| Prev | Next |