Simplifying Expressions to Solve Equations

Like terms are terms with the same variable(s) and the same power.

A good way to familiarize yourself with like terms is to compare and contrast :

Like terms	Unlike terms

Ex.1

Simplify by combining like terms :

1. 7x + 3x *A good way to look at the variables is making them a unit of measure. For
example, make the x a dollar and read it this way, “7 dollars + 3 dollars.” The answer is
obviously 10 dollars. It’s the same concept with variable terms. So 7x + 3x = 10x.

2. -5a + 2b -a + 3b *Because of the commutative property of addition (and remember that
subtraction is a form of addition), I can rearrange these terms if necessary. So putting my
like terms together gives me: -5a -a + 2b + 3b (notice that only the order changed , not
the signs). Now combining like terms gives me an answer of -6a + 5b.

Ex. 2

Use the distributive property to simplify:

1. 3(x + 2) *Normally in the order of operations, we would work operations inside the
parenthesis first , but in this case, x and 2 are not like terms and can not be combined. The
only way to simplify this expression is by using the distributive property. So we’ll
distribute the 3 this way: 3(x) + 3(2). Note that 3(x) is 3x and 3(2) is 6 so the answer is
3x + 6.

2. -2(y + 8) *Again, we would do the order of operations if possible, but this is not the case.
So we’ll use the distributive property to rewrite: -2(y) + -2(8) and we’ll get -2y -16 for
our answer. Remember that since subtraction is the opposite of addition, this could also
be written as -2y + -16 or -16 -2y.

3. 5(2a + 3) + 2(a -5) *The only difference with this expression is that we have two sets of
parentheses. Distribute the 5 through the first set of parenthesis and the 2 through the
second set to get: 5(2a) + 3 + 2(a) + 2(-5). This will leave us with 10a + 3 + 2a -10.
Unlike the others, we have like terms in this expression that can be combined (the 10a
and the 2a, etc.). You can rearrange if necessary and get: 10a + 2a + 3 -10. After
combining the like terms we get 12a -7.

Steps for solving linear equations :
1) Simplify the expression on each side of the equal sign ( clear fractions , clear parentheses,
combine like terms, etc.).
2) Get variable terms on one side of the equation and constants on the other.
3) Isolate the variable and solve the equation .
4) Check the solution .

Ex. 3

Solve each equation:

1. 3x + 6 -5x = 10 *This equation is unlike others that we have solved because we have two
variable terms in the equation. Looking at the steps for solving equations, we see that the
first step is to simplify the expressions on each side of the equal sign. I notice on the left
side, I have like terms that can be combined: -2x + 6 = 10. Now I move to step 2 and get
my variable terms (I only have one) on one side and constants on the other: -2x = 4
(remember to subtract 6 from both sides of the equation). Now I’ll isolate the variable by
dividing both sides of the equation by -2 and get x = -2. To check your solution, always
go back to the original equation: 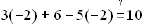. Using our order of
operations: -6 + 6 + 10 is indeed 10.

2. 2(4y -1) + 3(y + 2) = 11 *This time, before combining like terms we have to get rid of
the parentheses. We know that we do this using the distributive property:
8y -2 + 3y + 6 = 11. Now combining like terms gives us: 11y + 4 = 11. Now we get the
constants on the right side: 11y = 7. Isolate the variable to get  .

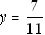Ex. 4

Solve each equation:

1. 3(2x -5) + 7 = 4(x + 9) *This equation is not too different from the example above but it
involves variable terms on each side of the equal sign. We’ll get to that in a minute.
First, get rid of the parentheses by using the distributive property: 6x -15 + 7 = 4x + 36.
On the left side of the equal sign, we have some like terms to combine: 6x -8 = 4x + 36.
At this point, we can’t add like terms (6x & 4x) until they are on the same side of the
equal sign. We’ll use the same procedure that we learned in section 2.1:

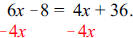	This step yields:

2x -8 = 36. Now this looks just like the equations in 2.2. We’ll get rid of the -8 by
adding it to both sides: 2x = 44. Finally, we’ll divide by 2 on both sides and get x = 22.