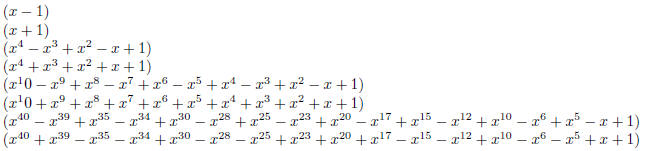Solutions to Math 2020 homework
Solutions to Math 2020 homework 2
To fit on the paper better, I’ll start with 4 first:
4. find a proof by contradiction for the statement “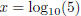 is irrational”,
using the following steps:
is irrational”,
using the following steps:
o. Aiming for a contradiction, assume x is rational . (The opposite (or negation)
of what we want to prove.)
i. Use the definition: What does it mean for x to be rational?
ii. Use the definition: What does it mean for
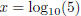 ?
?
iii. Put i and ii together, and use some properties of logatithms, e.g.,
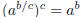 , so that from the equality
, so that from the equality
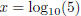 you get another equality, involving only integers, and using
notation introduced in steps i and ii .
you get another equality, involving only integers, and using
notation introduced in steps i and ii .
iv. Use a previous result , in this case, apply unique prime factorisation.
v. Derive a contradiction. This means that step o was wrong, so x is irrational.
QED
Proof that 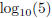 is irrational: is irrational:Suppose that x was rational. Then for some integers a, b, we have x = a/b. By definition, if 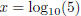 , then 10x = 5. , then 10x = 5.Note that since 5 is greater than 1, this means x must be positive, so a and b can also be taken to be positive. Substituting x = a/b into 10x = 5 gives 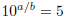 , now take b powers of both sides, to
get , now take b powers of both sides, to
get 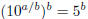 so so
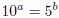 , ,where a and b are positive integers . But 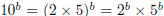 is even, and 5b is odd, so we have an odd
number equal to an even number, which is is even, and 5b is odd, so we have an odd
number equal to an even number, which isimpossible. So the original assumption that x is irrational must have been wrong. So x must be irrational. QED |
As discussed in the class before the homework is due, it’s
useful to do question 3 before question 1:
3. For any positive integer m, the polynomial (x − 1) divides x m − 1. What is
the quotient?
| First, note that (x − 1) does divide the
polynomial f (x) = xm − 1. This follows from the result that says that (x − a) is a factor of 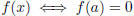 . .So, this means we can make the division, with no remainder. What we get is:
or in other words,
There are several ways to show this; we can use
long division of polynomials (which you should be able to do), or proof
|
As discussed in class, there is another useful factorisation to know, closely related to the above:
| If m is odd, then
or in other words,
This can be proved by a similar direct caclulation
as above, or else by substituting x = −t in the previous formula, |
1. Find the prime factorisations of
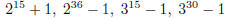
| Several factors can be found by applying the
formulas above :
You now need to check that 331 is prime, e.g., by
checking that it is not divisible by any prime up to
Note, here we had to factor 4033 by hand, by trial
and error — just try all the primes up to it’s square root . Then Other examples work similarly; the final solutions will be:
You’ll have to check that 4561 is prime by
checking whether it’s divisible by primes up to
|
2. Find four prime divisors of 34110 − 1.
| Using the same formulas as above, you can show
this is divisble by 34 − 1 = 33 = 3 × 11 and 34 + 1 = 35 = 5 × 7 — see example in lecture notes. So four factors are 3, 5, 7, 11.
It’s actually quite hard to get much further than
this. You can factor x110 − 1 further; you’ll get the following
These correspond to taking m = 2, 5, 11 in the
formulas, so this should not be too hard for you to find these factors. |
| Prev | Next |
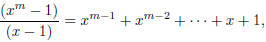
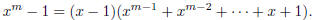
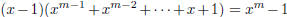
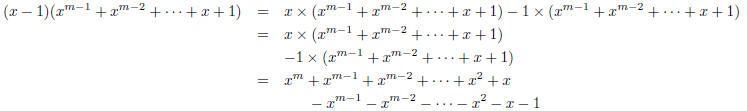
 (since all the
(since all the 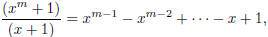
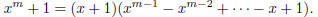
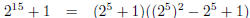 apply formula with m = 3
apply formula with m = 3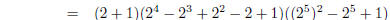 apply formula with m =
apply formula with m =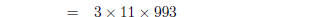
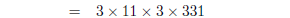 factor by hand
factor by hand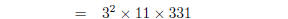 collect terms
collect terms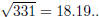
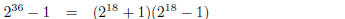 apply formula
with m = 2
apply formula
with m = 2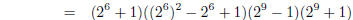 apply formula with m = 2 and m = 3
apply formula with m = 2 and m = 3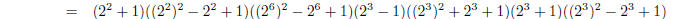
 apply formulas three times, with m =
3
apply formulas three times, with m =
3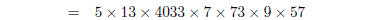 multiply out expressions in
multiply out expressions in 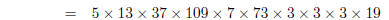 factor by hand
factor by hand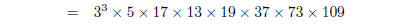 collect terms
collect terms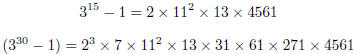
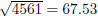 .
.