SOLVING EXPONENTIAL EQUATIONS
Problem 3:
Solve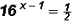 
Method 1:
Let's use the natural logarithm in the solution process!
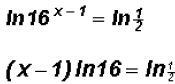Notice the parentheses
around (x - 1)!!!
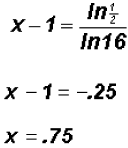
Method 2:
Please be aware that we can only use this method because the numbers
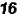
and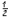 
have the same base when written in
exponential form . That is,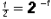
and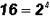 
.
Therefore, let's rewrite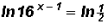 
as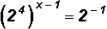 
and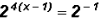 
Since the two expressions are obviously equal, and the bases are also
obviously equal, then the two exponents also MUST be equal to each other.
Therefore,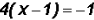
.
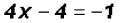
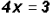and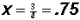 
Problem 4:
Solve: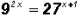 
not
using logarithms !
Let's solve this exponential equation using the fact that 9 and 27
have the same base!
That is,
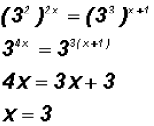
Problem 5:
Solve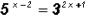 
. Round to 3 decimal places .
Let's use the common logarithm in the solution process !
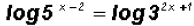
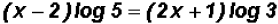
Next, we distribute the logarithmic expressions
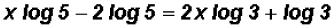
and collect the expressions containing the variable on one side
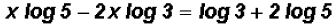
this allows us to factor out the variable and isolate it as follows
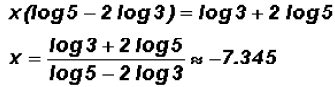
Problem 6:
How many years will it take for an initial investment of $10,000 to grow
to $25,000?
Assume a rate of interest of 2.5% compounded continuously. Round your
answer to a
whole number. Use the formula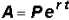 
, where P
is the initial investment, A is the
accumulated amount, t is the time in years and r is the interest rate in
decimals.
NOTE: Do not round until you find the final answer!
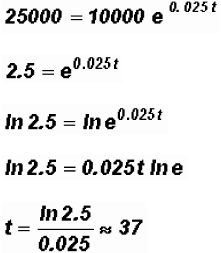
takes approximately 37 years for $10,000 to grow to
$25,000 at a rate of
interest of 2.5%.
Problem 7:
The number of bacteria A in a certain culture is given by the growth
model
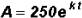. Find the growth constant k knowing
that A = 280 when t = 5. Round
your answer to four decimal places.
NOTE: Do not round until you find the final answer!
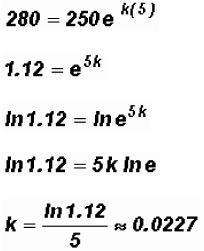
The growth constant k equals approximately 0.0227.
Problem 8:
The half-life of a radioactive substance is 950 years.. Find the constant
k rounded to
seven decimal places. Do not use scientific notation! Hint: Half-life means that
exactly
one-half of the original amount or size of the substance is left after a certain
number of
years of growth/decay. Use the Exponential Growth /Decay Model
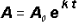, where
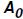is the original amount, A is the
accumulated amount, t is the time in years and k is the
growth constant.
We know that after 950 years one-half of the original amount
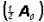is left. Therefore,
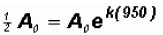
Then
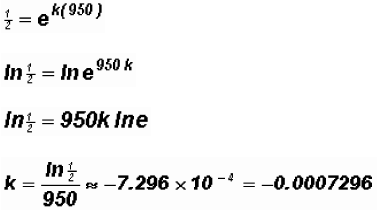
The decay constant k equals approximately - 0.0007296.
Problem 9:
The next problem involves carbon-14 dating which is used to determine the age of
fossils
and artifacts. The method is based on considering the percentage of a half-life
of carbon-
14 of approximately 5715 years. Specifically, the model for carbon-14 is
.
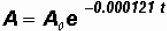In 1947, an Arab Bedouin herdsman found earthenware jars containing what are
known
as the Dead Sea scrolls. Analysis at that time indicated that the scroll
wrappings
contained 76% of their original carbon-14. Estimate the age of the scrolls in
1947.
Round your answer to a whole number.
We know that A, the amount present is 76% of the original amount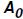
. Therefore, we
can use the model to write
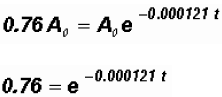
The Dead Sea Scrolls were approximately 2268 years old in 1947.
| Prev | Next |