Combining Functions and Iteration

Item 1.1. We have the ability to combine numbers in a multitude of ways: by
adding them , subtracting them, multiplying them, dividing them, raising them
to powers , etc. Can we do the same thing with functions? Of course we can!

Definition 1.2. Let f and g be functions of x. Then we can define the following
functions and their domains:

• (f + g)(x) = f(x) + g(x). The domain of (f + g) consists of all the real
numbers that are in the domain of f and in the domain of g.

• (f − g)(x) = f(x) − g(x). The domain of (f − g) consists of all the real
numbers that are in the domain of f and in the domain of g.

• (fg)(x) = f(x)g(x). The domain of (fg) consists of all the real numbers
that are in the domain of f and in the domain of g.

• (f/g)(x) = f(x)/g(x), g(x) ≠ 0. The domain of (f/g) consists of all the
real numbers that are in the domain of f and in the domain of g, and
that do not make g(x) = 0.

Example 1.3. Let f(x) = 3x+1, g(x) = 5x, and h(x) = 7x² +2. Compute the
following combinations :

• (f +g)(x). We have that (f +g)(x) = f(x)+g(x) = 3x+1+5x = 8x+1.

• (3f + 2g)(x). We have that

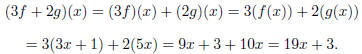
• (fh − g)(x). We have that



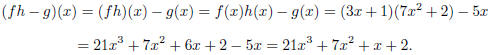
• ((f − g)/(f + g))(x). This gives us

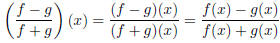
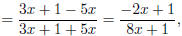whenever

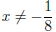
Item 1.4. There is another way that we can combine functions, as well. It
involves “piggybacking” functions by doing one function first, then “plugging
in” the output to the next function.

Example 1.5. Consider the following two tables of values:

Then, to find f(g(2)), we notice that g(2) = 3, and plug 3 into f : f(3) = 2.
Thus, (f o g)(2) = 2. To find g(f(2)), we notice that f(2) = 3, and g(3) = 4.
Thus, (g o f)(2) = 4. This reminds us that composition of functions is not
commutative, since we don’t get the same answer by switching the order of our
functions . Moreover, check that f(g(4)) = 4, and g(f(4)) is undefined.

Item 1.6. We can also do this by way of looking at the graphs of two functions.
To find g(f(2)), we first look at the graph of the innermost function, f(x), and
find its y− value at x = 2. We then take that value, and use it as the x−value
of the g graph. Finding the y−value here will give us the value of g(f(2)).

Item 1.7. Thirdly, we can find the composition of functions purely algebraically.
That is, we use the rules given for each function to find the rule given by their
composite. Consider the following examples.

Example 1.8. Let f(x) = 3x + 5x² and 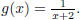Then we wish to find the
rule for g(f(x)), and the value for g(f(1)). To find the rule, we substitute in the
values for the innermost function first, then plug the whole expression into the
outermost function. So we have

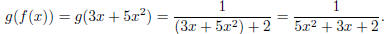
To find the value, we can either use this new rule, and see that

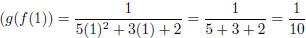
or we can proceed as we did when we considered f and g defined in a table:

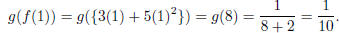
Example 1.9. Let f(x) = 2x² and 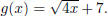Find f(g(x)) and f(g(4)).
To find the rule, we again substitute the innermost function into the next one,
as such:

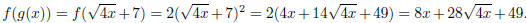
Then we have that f(g(4)) = 32 + 28(4) + 49 = 32 + 112 + 49 = 193.

Definition 1.10. An iteration is a special type of composition; it is the composition
of a function with itself a certain number of times . The idea of iteration
corresponds roughly to the exponentiation of real numbers.

Example 1.11. Let 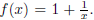Then we can find the “second iteration of
f” by composing f with itself:

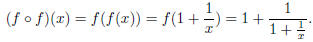
We will want to simplify this horrendous beast, in case we need to find the value
for the second iteration:

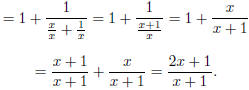
Thus, we have a rule for the second iteration of f, and we find that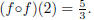

Item 1.12. We need to say a word about the composition of functions here.
The domain of composition must respect the domains of both functions in the
order they are given. What exactly does this mean? If we are looking at the
composition f(g(x)), the x-values living in the domain are the ones that we can
use for g, and the ones that give an acceptable g(x)−value that we can plug into
f. Let us explore this with an example.

Example 1.13. Let f(x) = 3x²+1, and 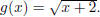We notice the following
restrictions on domain and range:

Function	Domain	Range

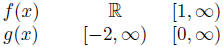Notice also that (f o g)(x) = 3x+7. It looks like we can plug any real number in
for x, but we have to realize where this function comes from. Notice that we are
not allowed to plug in any number less than −2 for x, since it would make g(x),
and therefore our composition, undefined. So for the composition, we actually
have

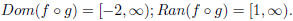
Item 1.14. Now that we feel completely comfortable finding a composition of
functions, we can think about splitting up existing functions into composite
functions. To do so, we think of the functions in the order that we would use to
evaluate a y−value for any given x−value.

Example 1.15. Write the function H(x) = (2x + 5)³ as a composition of
functions. If we were to evaluate H(1), say, we would compute the expression
on the inside of the parentheses first , right? So, let g(x) = 2x + 5. Afterward
that computation, we would cube the result . So let f(x) = x³. Then, composing
these two functions , we can see that

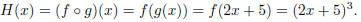
Example 1.16. Check that if 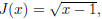then, letting f(x) = x−1, g(x) =
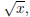we will have that

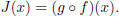
Also, notice that these compositions are by no means unique. Let h(x) = x + 2,
and 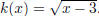Check also that

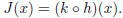
Item 1.17. Let us wrap up this section by doing one example that incorporates
all of the functions we learned today.

Example 1.18. Define the functions f, g, h, and k as follows:

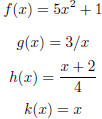
Find the formula for the function

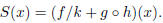
So we have

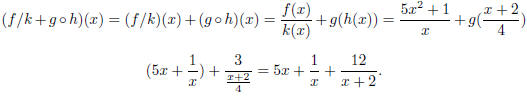
Item 1.19. Please do the following problems for homework. They can be found
on page 224ff., and will be due on Monday.

7, 13, 19, 27, 31, 53