Complex Numbers and the Complex Exponential

3 Polar Form

The set of points at unit distance from the origin in the complex plane , corresponding to
the complex numbers z with |z| = 1, form a circle of unit radius centered at the origin. This
circle is called the unit circle in the complex plane. Every point on the unit circle can be
represented in the form z = cos θ+ j sin θ, where (from now on) θ represents an angle.

More generally, as illustrated in Fig. 1(b), a complex number z = a + b j can be represented
in the polar form



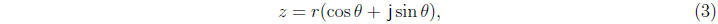
where r = |z| and, if z ≠ 0, cos θ = Re(z)/|z| and sin θ = Im(z)/|z|. The angle θ is called
the argument or phase of z, and is denoted arg(z). The phase of z = 0 is not defined.

Now, since cos(x) and sin(x) are periodic with period 2π , it is clear that if 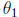is a value of
arg (z), then so are 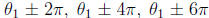, and so on. Thus arg(z) does not specify a
unique angle, but rather it specifies an infinite class of equivalent angles, each differing from
the others by some integer multiple of 2π . For example,



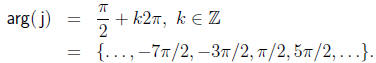
So that every complex number has a unique phase, we can select an angle from any half-open
interval I of the real numbers of length 2π , so that it is impossible for more than one angle
from each equivalence class to fall in I. By convention, this interval is usually chosen as
 (-π , π], and the corresponding angle is referred to as the principal value of the argument,
denoted Arg(z), or ∠z. Note the capital letter: whereas arg(z) denotes an infinite set of
equivalent angles, Arg(z) specifies a unique angle in the range (-π , π]. Thus, for example,


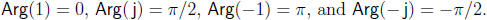
Although polar form is an inconvenient representation for complex addition, it is great for
multiplication. Indeed, if we multiply 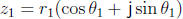with ,
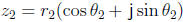we get



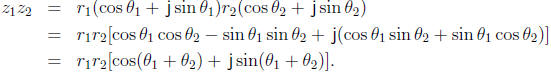
We see that under complex multiplication, magnitudes multiply and phases add, i.e.,



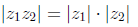
and



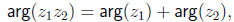
where the latter equality is interpreted in the following way: if we substitute a specific angle
for 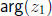and a specific angle for 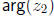, their sum is a member of the equivalence class of
angles of .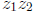

Now, if z ≠ 0, we have z(1/z) = 1; this means that if z has the polar form ,
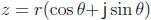then 1/z must have the polar form



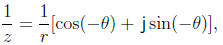
so that their product has the polar form 1 = 1(cos 0 + j sin 0). Thus taking reciprocals in
polar form is just as convenient as complex multiplication. It follows from this that if 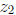≠ 0

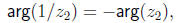
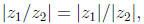
and

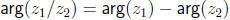, provided 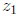≠ 0.

The property that the phase of a product is the sum of the phases is very reminiscent of
the rule for multiplying exponentials, where the exponent of a product is the sum of the
exponents, i.e., 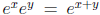. As we will see in the next section, where we consider the
complex exponential function, this connection is not a coincidence.

4 The Complex Exponential

To define a complex exponential function e^z, we would certainly wish to mimic some of the
familiar properties of the real exponential function; e.g., e^z should satisfy, for all 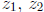and
z,



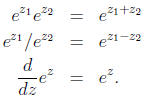
(The last equation requires that we first define what we mean by complex differentiation,
something that is beyond the scope of these notes. However, see, e.g., [1, 2].) Here we will
introduce the complex exponential in a sneaky way: via its Maclaurin series. (Recall that
the Maclaurin series of a function is the Taylor expansion of the function around zero .)

Recall that the real-valued functions cos(x), sin(x), and e^x have Maclaurin series given,
respectively, by



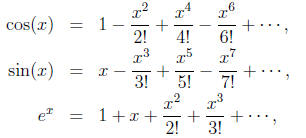
and that each of these series is convergent for every value of x ∈ R.

It would be natural indeed to define

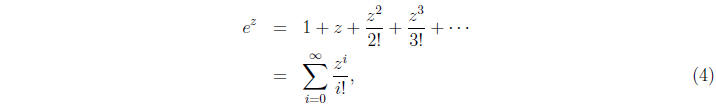
and this is precisely what we will do. Although we will not prove this here, the Maclaurin
series (4) is convergent for every value of z ∈ C. Clearly this complex-valued exponential
agrees with the usual real-valued exponential at every point z on the real-axis in the complex
plane.

To see that 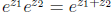, we multiply the corresponding Maclaurin series. This method of
multiplying series is sometimes called the Cauchy product. We want to form

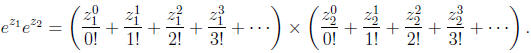
Using the distributive law and grouping terms having the same total exponent (sum of
exponent and exponent), we get

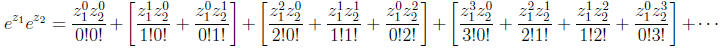
This sum can be written as

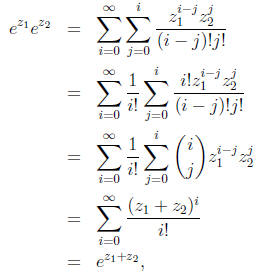
where, in the second last equality, we have made use of the binomial expansion (which holds
in any field).

Now, writing z = a + jb, with a ∈ R and b ∈ R, we find that

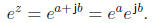
Since e^a is a (well understood) real-valued exponential, we see that the key to understanding
the complex-valued exponential is to understand the function e^jb for real b.

For this, we apply the Maclaurin series. We have, for real b,

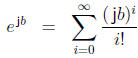
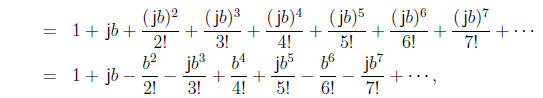
where we have used the fact that j² = -1, j³ = -j, j⁴ = 1, etc. Grouping the real and
imaginary parts, we find that, for real b,

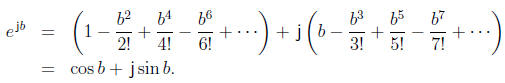
Thus we find that e^jb is essentially a trigonometric function: it has real part cos b and
imaginary part sin b. Applied to z = a + jb, the complex exponential returns

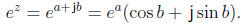
Using the complex exponential allows us to write, in a more compact way, the polar form
(3) of a complex number having magnitude r and phase θ we have

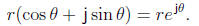
The fact that phases add under complex multiplication now becomes obvious, since

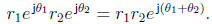
Since cos(- θ) = cos(θ ) and sin(-θ ) = -sin(θ ), we have

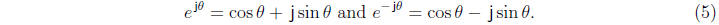
Adding the two equations in (5) yields 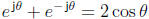, or

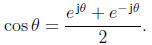
Subtracting the two equations in (5) yields 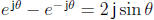, or

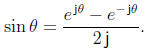
These relationships often allow one to derive various trigonometric identities via the complex
exponential function.