Determinant of a Matrix
The determinant of a matrix m can be found using the
command det.
Ex:
>> m=[1 3 2;6 4 7;0 9 3]
m =
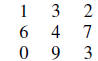
>> det(m)
ans =
3
Inverse of a Matrix.
The inverse of a matrix can be found using the command inv.
Ex:
m as before
>> inv(m)
ans =
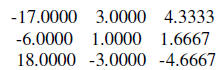
How to solve Systems of equations in MATLAB
Consider a linear equation
ax + by = p
cx + dy = q
We can write this more compactly as
AX = B
A is a matrix consisting of the coefficients of x and y .a b
c d
X is the vector of unknowns
x
y
B is the vector on the right-hand side is
p
q
If A is invertible, X = (1/A)B, or, using Matlab notation, X = A\B.
Example:
Find the solution of the following set of linear equations
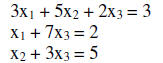
How to solve?
Express system of linear equations in the form of ax = b and then solve with \
command
in matlab. You can use the backslash operator to solve a system of simultaneous
linear
equations.
>> a= [3 5 2;1 0 7;0 1 3]
a =

>> b= [3;2;5]
b =
3
2
5
>> x=a\b
x =
-3.7647
2.5294
0.8235
Or you can type
>>x=inv(a)*b
You can check your answer by typing a*x in the command
window. You will get the
same values in b .
Back substitution.
The back Substitution method is used to solve Upper
triangular Linear systems .
For example:
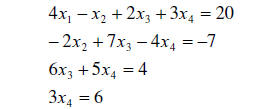
To solve this system we use back substitution:
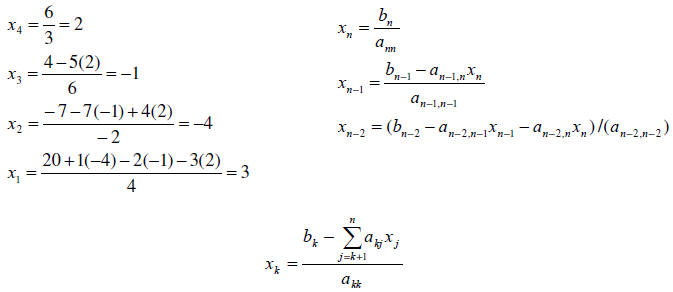
The following code uses the back substitution to solve upper-triangular linear systems:
function X=backsub(A,B)
%Input - A is an n x n upper-triangular nonsingular matrix
% - B is an n x 1 matrix
%Output - X is the solution to the linear system AX = B
n=length(B); % finds the length of vector B
X=zeros(n,1); % build a matrix X of dimensions (n,1) and zero elements
X(n)=B(n)/A(n,n); % evaluate the value of X in the last row
for k=n-1:-1:1 % starts calculating the values of x
X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k); % A(k,k+1:n) selects the
%elements k+1 to n in row k, X(k+1:n) selects the elements k+1 to n in
% the vector matrix X.
end
%Comment: to test the code enter in Matlab window (without
the %
signs):
%U = [4 -1 2 3; 0 -2 7 -4; 0 0 6 5; 0 0 0 3]
%Y = [20 -7 4 6]'
%X=backsub(U,Y)
% compare to the correct answer in Example 3.12, page 122
Trivial Pivoting
It is a pivoting strategy used when aii=0 (during Gauss
Elimination method).
When this happens, Find a row after the row i in which aki doesnt equal zero and
interchange these rows.
Ex:

To eliminate the elements in the first column in second
and third rows we multiply the
first row with 2 and subtract the result from the second row. Then we multiply
it with 3
and subtract the result from the third row to get the following matrix.

The 2,2 element is zero, we cant continue the process
unless we interchange the second
and the third rows to get

Partial Pivoting
The partial pivoting is used to reduce the error when
using Gauss Elimination method by
moving the elements with the highest absolute value to the diagonal.
Ex:

Interchange the first and the third columns

Interchange the 4th and the 2nd columns
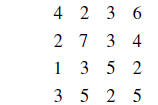
This is the best order for Gauss elimination method.
Partial Pivoting Code
The following code uses partial pivoting in Gauss elimination method to solve a
system
of linear equations.
In the code:
1) The size of a is defined and the matrix X is initiated.
2) The augmented matrix [A l B] is built.
3) Interchanging rows and elimination.
4) Call back substitution function to solve the system.
function X = partialpivoting(A,B)
format short e
%Input - A is an N x N nonsingular matrix
% - B is an N x 1 matrix
%Output - X is an N x 1 matrix containing the solution to AX=B.
%Initialize X and the temporary storage matrix C
[N N]=size(A); % [n m]=size(a) gives n: no. of rows, m: no. of columns,
% he didn’t say N=size(A), because that would give an array with N
%values
X=zeros(N,1);
C=zeros(1,N+1); % N+1 because it’s for augmented matrix
%Form the augmented matrix: Aug=[A|B]
Aug=[A B];
for p=1:N-1 % to N-1 because when we have 1 coloum left,
no pivoting
%is possible
%Partial pivoting for column p
[Y,j]=max(abs(Aug(p:N,p))); % finds the maximum absolute
value of
%the elements of row p in the augmented matrix, the value of the
%largest element is stored in Y, the position of the that element in
%the column is stored into j.
%Interchange row p and j
C=Aug(p,:); % saves the row p in c
Aug(p,:)=Aug(j+p-1,:); % saves the row j+p-1 in row p of aug matrix
Aug(j+p-1,:)=C; % moves the row in c to j+p-1 row in aug matrix
if Aug(p,p)==0
'A was singular. No unique solution'
Break % break is used to terminate FOR loops
end
%Elimination process for column p
for k=p+1:N
m=Aug(k,p)/Aug(p,p);
Aug(k,p:N+1)=Aug(k,p:N+1)-m*Aug(p,p:N+1);
end
end
%Back Substitution on [U|Y] using Program 3.1
X=backsub(Aug(1:N,1:N),Aug(1:N,N+1));
% Aug(1:N,1:N) constructs a matrix using the rows from 1 to N and
%columns from 1 to N (equals A matrix). Aug(1:N,N+1) builds a matrix
%using the elements in column N+1 (equals B matrix).
In the command window type:
A = [1 2 1 4; 2 0 4 3; 4 2 2 1; -3 1 3 2]
B = [13 28 20 6]'
X = partialpivoting(A,B)
Compare to the correct answer in Example 3.16, page 128
| Prev | Next |