Discrete Mathematical Structures Homework 0 Solutions
Grading: The questions on this homework have a total value
of 52 points but 12 points
will be considered bonus points (i.e. score of 40 or higher will receive full
credit).
These questions asked only for short answers. An
explanation isn't required for full credit,
though it may help you get partial credit if your short answer is wrong.
1. [12 points] Simplify the following expressions as much
as possible, without using a calcu-
lator (either hardware or software). Do not approximate. Express all rational
numbers as
improper fractions.
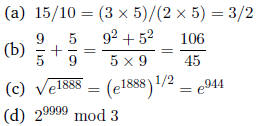
For this problem, remember the following identities:
(a) ab mod m ≡ ((a mod m) × (b mod m)) mod m
(b) if a ≡ b then an ≡ bn mod m
First, we can write 29999 as 21+9998 = 2(29998) = 2(22×4999)
= 2((22)4999)) = 2(44999).
Using the identity (a), we have:
2(44999) ≡ ((2 mod 3) × (44999 mod 3)) mod 3.
Given that 4 ≡ 1 mod 3, using the identity (b):
44999 ≡ 14999 mod 3 = 1 mod 3.
Thus:
29999
≡2(44999) mod 3
≡ ((2 mod 3) × (44999 mod 3)) mod 3
≡ ((2 mod 3) × (1 mod 3)) mod 3
≡ ((2 mod 3) × 1) mod 3
≡ 2 mod 3 = 2
Another way to attack this problem is to compute 2n mod 3
for a number of small values
of n. The value is 2 if n is odd and 1 if n is even. We'll see later that an
inductive proof
can formalize this approach.
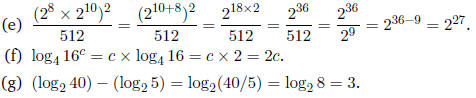

Using synthetic division as :
We have:
Thus
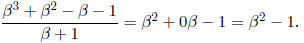
Or you could factor the top into
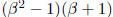 and then cancel the
and then cancel the
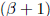 terms.
terms.
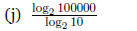
From the identity
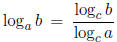 (often used for changing the base of a logarithm),
(often used for changing the base of a logarithm),
setting a = 10, b = 100000, and c = 2, we have:
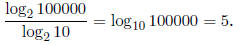
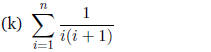
First, using partial fractions:
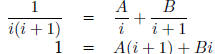 Multiplying both sides of the equation by i(i + 1)
Multiplying both sides of the equation by i(i + 1)
 Setting
i = 0
Setting
i = 0
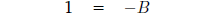 Setting i = -1
Setting i = -1
Now we have:
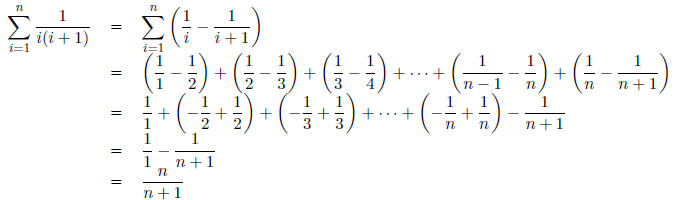
Another approach is to compute the value of the summation
for the first few values of n,
adding together the fractions and simplifying the result. The first few values
are: 1/2 , 2/3 ,
3/4 , 4/5 . The formula is then obvious. Mathematical induction (see later this
course) could
be used to prove it's correct.
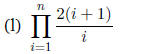

2. [10 points] Suppose we have the following sets:
A = ,
,
B = {1, 2, 3}
C = {3, 4, 5}
D = Z
Note: Z denotes the set of integer numbers.
(a) What is (D ∩ C) ∪
B ?
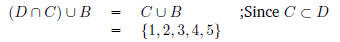
(b) What is (B ∪ D ∩
A) ∪ C?
This formula is actually ambiguous. Another set of parentheses would be required
to indicate
whether the first union or the first intersection is done first. Either of the
answers is ok for full
credit, explaining the ambiguity is worth 1 point bonus.
Assuming ∪ takes precedence over ∩:
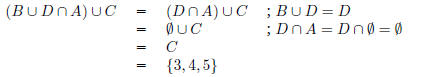
Assuming ∩ takes precedence over
∪:
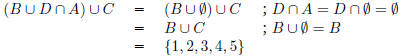
(c) What is (D ∩B ∩
C) ∪D?
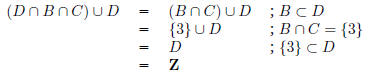
(d) What is (D - B) ∩ C?
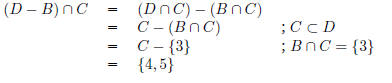
3. [10 points] Suppose F(x) = x3 - 5x and G(x) = x + 4 and H(x) = sin x.
(a) What is F(G(z))?
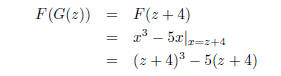
(b) What is G(G(G(G(G(10)))))?

(c) What is H(G(F(1))) × F(G(H(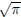 )))?
)))?
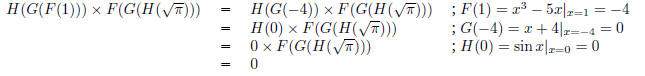
4. [10 points] There is a popular and unverifiable story
that Carl Friedrich Gauss (mathematician, 1777-
1855) had a lazy teacher while in grade school. In order to keep the students
busy so he could take a
nap, the teacher asked the class to add the numbers 1 to 100. To the profound
disappointment of the
teacher, Gauss was able to do this in less than a minute...and you can, too.
(a) What is the sum of the numbers 1 to 100?
Hint: Imagine writing out the numbers 1 to 100 in one row and then in a second
row reversing
the order and writing the numbers from 100 down to 1:

Then, add the numbers in each column and see if you notice
a pattern.
Answer. After adding each column we have that (1 + 100) = (2 + 99) = (3 + 98) …
= 101. We
have 100 such columns, which added together yield 100 ×
101 = 10100. When we added all of
the columns, each number was added twice (for example, the first and last
columns have the
numbers 1 and 100, the second and second to last columns have the numbers 2 and
99, and so
on). Thus, dividing 10100 by 2 yields our result: 10100/2 = 5050.
(b) Write an expression for the sum of the numbers from 1
to n using summation notation. Your
answer should look like
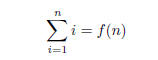
where f(n) is a simple function that yields the sum of the
first n numbers for any positive integer
n.
Answer. Generalizing the pattern we discovered before, we
have:
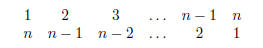
The value of each column is n + 1, and we have n of such
columns. Adding all of the columns
together yields n(n + 1). Again, given that each number was added twice.
dividing by 2 gives the
desired formula:
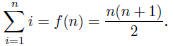
5. [10 points] The word algorithm, derived from the name
of the ninth-century Persian mathematician
 refers to a step-by- step method for solving a problem. Consider the following
algorithm
refers to a step-by- step method for solving a problem. Consider the following
algorithm
for solving a problem:
Input: A positive integer number a
Output: A positive integer number s
Let s = 0
While a > 0
Let s = s + (a mod 10)
Let a = a/10
In this algorithm, the word while indicates a loop,
meaning that following indented steps are repeated
as long as the loop condition of a > 0 holds. Also, note the operation a/10 is
integer division, meaning
that the fractional portion of the result is simply dropped (e.g. 10/4 = 2).
(a) What is the output of the algorithm if the input is a
= 432765891
Answer. First, we observe a few iterations of the while-loop, to understand what
the pseudo-code
given is doing:

From these first iterations, we can observe that digits
originally in a are added one by one into
s. After the number '4' in a is added, a = 0. This terminates the algorithm ,
given the condition
a > 0 in the while-loop. The value of s obtained is:
s = 4 + 3 + 2 + 7 + 6 + 5 + 8 + 9 + 1 = 45
(b) One important characteristic of an algorithm is
efficiency. Typically, this is measured by the
number of operations the algorithm performs. How many additions does this
algorithm perform
given the input of some positive integer a? Express your answer as a function of
a.
Answer. There is one iteration of the while-loop per digit originally in a.
Thus, to answer the
question we should study the structure of the number given in a. In our example
a = 432765891,
which can be written as:

After the first iteration, we have:
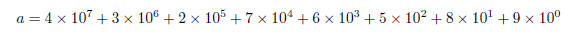
Notice that after the iteration, the exponents decreased
by one, and the term 1 × 100 disappeared.
With this in mind, let's take a look at the value of a at the last iteration:
a = 4 × 100
The exponent went from 8 in 4 ×
108, to 0 in 4 × 100. Therefore, the while-loop
repeated exactly
9 times. Generalizing to any number given in a, this means that if we know the
exponent of the
maximum power of 10 that fits in a, and we add 1 to such exponent, we know how
many times
the while-loop repeats. For example, if a = 312 = 3 ×
102 +1 × 101 +2 × 100, now we
expect the
while-loop to repeat 3 times .
The value of this exponent can be obtained computing
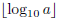 In this expression,
In this expression,
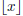 gives the
gives the
largest integer smaller than or equal to x (i.e.,
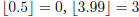 ).
Now we conclude that the
).
Now we conclude that the
number of additions performed by the algorithm is
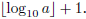
Both
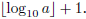 and number of digits in a are reasonable full-credit answers to this question,
and number of digits in a are reasonable full-credit answers to this question,
at this point in your career. As we start discussion big-O notation, and
especially when you take
the algorithms class, you find that instructors expect the answer using the
logarithm.
| Prev | Next |