Donuts and Cubic Function Fields
Overview
* Motivation
* Brief History of Public Key Crypto
* Must Go Faster
* Real vs . Imaginary Curves
* Infrastructure
* Function Fields
* Computational Stuff
* Won't You Be my i-Neighbor?
* Finding Two Fundamental Units
* Examples
* Two Fundamental Units
* The Donut
Motivation
The goal of my research is to study cubic function
fields as a new setting for cryptography.
We never know if or when existing cryptosystems
are going to be broken or weakened, so
it's wise to have some uncracked ones laying
around.
Even if cubic function fields are never used or
their use is found to be insecure, we can always
take of the cryptographer's hat and put
on the computational number theorist 's hat.
There are interesting theoretical questions that
arise in studying these fields, many of which are
needed for crypto.
Crypto Needs:
* Group, efficient representation and arithmetic
* Group order with large prime divisor
* Efficient computation of the group order
* Security based on a \hard problem"
History
* RSA published (publicly) in 1977
* 129- digit challenge problem
* Estimated over 40 quadrillion years to break.
* 1991: Quadratic Sieve - subexponential time
factoring: L[1/2; 1]
* 1994: Actual time to solve the challenge : 8
months
* "The magic words are squeamish ossifrage."
* 1993: Number Field Sieve - asymptotically
much faster than QS: L[1/3, 1.92…]
* 1985: Elliptic Curve Cryptography
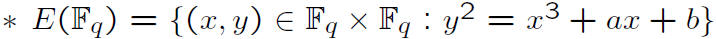
* ECC based on the Discrete Log Problem :
* Given two points P and Q, find k such that
kP = Q.
* Fastest known algorithm to solve it, Pollard's
Rho, runs in exponential time.
Must Go Faster
* Since the ECDLP is harder than factoring ,
key sizes for ECC are smaller than for RSA.
* Smaller keys mean faster arithmetic.
* Elliptic curves are genus 1; they are donuts.
*
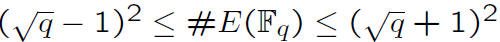
* 1989: Hyperelliptic Curve Cryptography
*
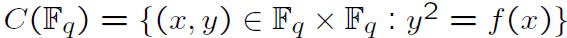
* Group law is different . Look at the Jaco-bian.
* For a curve C of genus g over Fq:
*
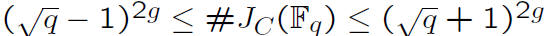
* A large genus means a small q and small
keys!
* Genus of C is g if deg f = 2g +1 or 2g +2.
* The DLP is faster than Rho for g ≥ 4.
* Can cubic, y3 = f(x), curves run faster?
Real vs. Imaginary Curves
Huh?
* Consider real and imaginary number fields
* What are some differences ?
Ideal class groups:
* Small (usually 1) for real fields.
* Large
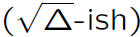for imaginary fields.
This makes the class group of an imaginary
field a good setting in which to do crypto.
Unit groups:
* Rank 0 for imaginary number fields.
* Maximal rank for real number fields.
* Degree d = r +2s, unit rank = r +s - 1
* The unit group is the best distinction.
* Function fields, extensions of Fq(x), not Q,
can have unit rank 0, 1, ..., d -1 depending on
how the point at infinity splits.
If real fields have a tiny ideal class group, what
good are they for cryptography?
Infrastructure
* Like railroads , interstates, and airports, right?
* Nope.
* For the class group of an imaginary quadratic
field, each ideal has a unique reduced representation ,
which makes things nice.
* In a real quadratic field, the principal class
(i.e. the ideal (1) = OK) does not have a
unique reduced form.
* Shanks noticed that the reduced principal
ideals had a group-like structure inside, a cycle
of reduced principal ideals which he called the
infrastructure.
* Arithmetic is via baby steps (like adding 1 in
F q) and giant steps (multiplying two ideals).
* The infrastructure can be used to compute
the fundamental unit of OK.
Function Fields
*
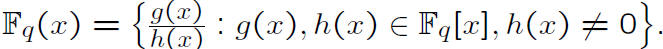
* A quadratic function field adjoins y, where
y2 = f(x) and is thus an elliptic or hyperelliptic
function field.
* If deg(f) is even, then the function field is
real, and there is an infrastructure and fundamental
unit.
* Else, arithmetic in the ideal class group cor-responds
to arithmetic in the Jacobian.
* By adjoining y where y3 = f(x), we have
a (purely) cubic function field.
* If q ≡ 1 mod 3, deg f = 6, f has a double
root , then the function field is real of genus 3,
so it has 2 units.
* The curve y3 = f(x) is a real Picard curve.
Computational Stuff
* The group order of Jacobians and such is
important to find and find quickly.
* Can search the interval of the range of Jacobians:
exponential time.
* In function fields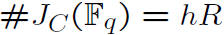
h = ideal class number = #Cl(K)
R = Regulator - which is based on the units.
* If
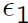and
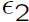are the two fundamental units
and
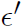denotes a nontrivial real embedding of
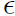, then
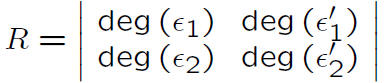
* Other approaches to finding the size of the
Jacobian involve the L- polynomial of the curve :
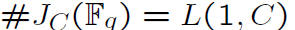and
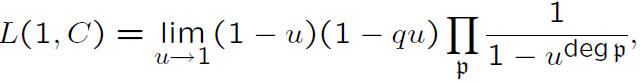
where p is a prime ideal in OK.
| Prev | Next |