Factoring
Basics

What is factoring anyway ?

Recall that that¡­

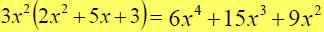
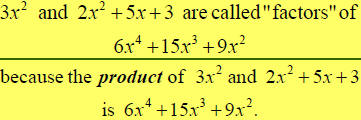
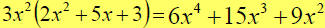
When you are ¡°factoring¡±a polynomial, you are finding its ¡°factors¡±.

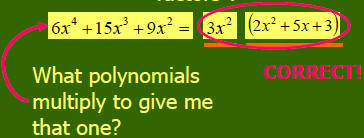
What polynomials multiply to give me that one?

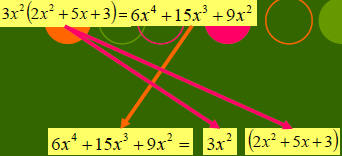
Factoring is the REVERSE of multiplication!

Completely Factored Form

A polynomial is said to be in completely factored form if¡­

1. The polynomial is The polynomial is expressed as a product expressed as a product
of polynomials with integral coefficients. of polynomials with integral coefficients.
2. 2. None of the factors None of the factors (except monomials) (except monomials)
can be factored again can be factored again into polynomials into polynomials
with integral coefficients.

There are many different factoring
methods methods ¡­

•Factoring Out the Highest Common Factoring Out the Highest Common
Monomial Factor Monomial Factor (Always try this method (Always try this method
first!) first!)
•Factoring By Grouping Factoring By Grouping
• Difference of Squares Difference of Squares
  Sum/Difference of Cubes Sum /Difference of Cubes
•Factoring Trinomials Factoring Trinomials
••With an x With an x^2 coefficient of 1 coefficient of 1
••With an x With an x^2 coefficient greater than 1 coefficient greater than 1

Where do I start?

• ALWAYS factor out any ALWAYS factor out any ¡°common factors common factors¡±
in each term first if possible. in each term first if possible.
••If you factored out a common factor, can the If you factored out a common factor, can the
remaining polynomial be factored again?? remaining polynomial be factored again??
••Next Next, ask yourself the question, , ask yourself the question, ¡°How How
many terms does the polynomial have? many terms does the polynomial have?¡±
(That should clue you in on what factoring (That should clue you in on what factoring
method might be used.)

How many terms does it have?

• Two terms Two terms ¨C You might try You might try¡­
••Difference of two squares pattern , p. 137 Difference of two squares pattern, p. 137
•• Sum of two cubes pattern, p. 139 Sum of two cubes pattern, p. 139
••Difference of two cubes pattern , p. 139

How many terms does it have?

• Three terms Three terms ¨C Use trinomial factoring Use trinomial factoring
techniques, p. 144

How many terms does it have?

• Four terms Four terms ¨C You might try factoring by You might try factoring by
grouping grouping
Can any factors be factored again? Can any factors be factored again?
Be sure to factor completely.

Keep in mind mind¡­

• Always check for common factors first
• Factor completely!
•There will be a specific factoring method
to use when factoring a polynomial. Make
a habit of recognizing what method will be
used and then using the proper method.

Practice Problems

• Page 160, # 24 24-45
Special instructions: For each problem, write the name of
the factoring method that you are going to use before
you use it.
Answers are in the back of the book. Please do not get in
a habit of looking at the answers before you work the
problem ¨C it tends to hurt more than it helps.
• ThomsonNow ThomsonNow: Get registered before next class!
(10 points)
• ThomsonNow ThomsonNow: Factoring Worksheet