Hints for quadratic equation

You can use the discussion board to post questions and/or read responses. Josh will be live
on that board MWF from 7-8 pm all semester. If you post a question at a different time ,
he will respond as soon as he is able. Do not post after 8:00 pm on a due night and
expect an immediate answer. He will not help you as a tutor, but may provide some
hints. Please do not expect him to solve things for you.

In general, use Mozilla browser with a PC. Internet Explorer can cause technical issues
with Cengage Now problems. We recommend using an ITAP computer or following the
configuration instructions on the Cengage Now homepage.
If you log in and see a message that says popups are blocked, enter Cengage Now
anyway. That error does not affect your assignments. However, a current version of Java
must be installed for Cengage Now to work properly. If the system check detects a Java
problem, follow the instructions given to correct that.

You can always view the correct answer to each problem after submitting the assignment.
Click on “view assignment details”. It will show you what you entered and what the
correct answer was. If you log back into the assignment, you will get a different version
of the problems that were not correct. Correct problems stay correct and you do not redo
them.

Lesson 14:

#3: Math hint : Remember to always check for extraneous solutions when squaring both
sides of an equation

#4, #5, #6: Math hint: After squaring both sides and getting all terms to one side of the
equation, the resulting quadratic equation will factor by trial and error. Remember to
always check for extraneous solutions when squaring both sides of an equation.

#7: Math hint: This equation will factor by trial and error but you could also use the
quadratic formula. If you use the quadratic formula, remember to have:

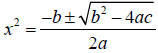
and simplify. Then, lastly, you will need to square root both
answers to solve the equation.

#8: Math hint: You must use the quadratic formula (or completing the square) to solve
this equation. Again, remember to have:

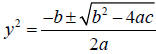
and simplify. Then, lastly, you will need to square root both
answers to solve the equation.

#9, #10, #11: These are all parts of #52 from the textbook. Math hint: If you take an
even root of both sides of an equation, you need to include the plus/minus root. If you
raise both sides of an equation to an even power , there is the possibility of extraneous
solutions. Break these equations into two steps . Raise both sides first, then take
whichever root is needed second.

#13: Math hint: The formula needed for this problem is the surface area of a cone (given
on a quiz or exam if needed):

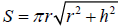
Leave your answer in as exact (do not round to a decimal approximation ). This is a
difficult problem. See a similar example in class.

Lesson 15
In general, you must use interval notation in the majority of answers. Always write the
interval notation from smallest number to largest number. For example, it is not correct
to write an interval as [7,∞)∪[3,7]. This would be counted as incorrect. It must be
written as [3,7]∪[7,∞). This would be true in class also, not just on the computer. Use
cup for the ∪ symbol , inf for ∞, and –inf for − ∞.

#1: Use inequalities (not interval notation).

#5: Remember to write interval notation in order from smallest number to largest number.

#6 and #7: This is a notation question, so it want the inequality (not interval notation).

#17: The absolute value tool is under the toolbar in the bottom right corner. The
subscript tool is under the log x toolbar in the top right corner.

#18: Use the inequality for the answer (not interval notation).

#19: Use the inequality for the answer (not interval notation). Also, use fractions and not
decimal approximations.

#20: Answer will be a number only (no inequality or interval notation needed).

Lesson 16

#4: Remember simplify the radical if possible

#7: Math hint: Use the distance formula to find the length of each side of the triangle.
All ordered pairs are integers (no fractions are used). You can eyeball which of the three
angles is the right angle (90 degrees). Then use A = (1/2)bh to calculate the area. Simplify
this result (it should work out to a nice number).

#11: Math hint: Use the distance formula with two points given and set equal to the
distance given. Square both side and solve for a. The quadratic equation WILL factor by
trial and error. Remember which quadrant the point needed and disregard the solution
that would be in the wrong quadrant. Calculate the coordinates with the remaining
solution for the final answers.