Hyperbolas
Identify the type of conic section (parabola, ellipse,
circle, or hyperbola) represented by each of the
following equations. (In the case of a circle, identify
the conic section as a circle rather than an ellipse.) Do
NOT write the equations in standard form; these
questions can instead be answered by looking at the
signs of the quadratic terms .
1. 2y + x2 + 9x = 0
2. 14x2 + 7x −12y = −6y2 + 95
3. 7x2 − 3y2 = 5x − y + 40
4. y2 + 9 = 9y − x
5. 3x2 − 7x + 3y2 = −12y +13
6. x2 +10x = −2y − y2 + 5
7. 4y2 + 2x2 = 8y − 6x + 9
8. 8y2 + 24x = 8x2 + 30
Write each of the following equations in the standard
form for the equation of a hyperbola, where the
standard form is represented by one of the following
equations:
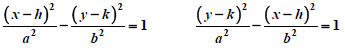
9. y2 −8x2 −8 = 0
10. 3x2 −10y2 − 30 = 0
11. x2 − y2 − 6x = −2y − 3
12. 9x2 − 3y2 = 48y +192
13. 7x2 − 5y2 +14x + 20y − 48 = 0
14. 9y2 − 2x2 + 90y +16x +175 = 0
Answer the following.
15. The length of the transverse axis of a hyperbola
is __________.
16. The length of the conjugate axis of a hyperbola is
__________.
17. The following questions establish the formulas
for the slant asymptotes of
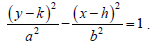
(a) State the point- slope equation for a line.
(b) Substitute the center of the hyperbola,
(h, k ) into the equation from part (a).
(c) Recall that the formula for slope is
represented by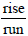 
. In the equation
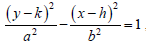, what is the “rise” of
each slant asymptote from the center? What
is the “run” of each slant asymptote from the
center?
(d) Based on the answers to part (c), what is the
slope of each of the asymptotes for the graph
of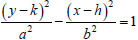 
? (Remember that
there are two slant asymptotes passing
through the center of the hyperbola, one
having positive slope and one having
negative slope .)
(e) Substitute the slopes from part (d) into the
equation from part (b) to obtain the
equations of the slant asymptotes.
18. The following questions establish the formulas
for the slant asymptotes of
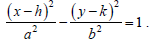
(a) State the point-slope equation for a line .
(b) Substitute the center of the hyperbola,
(h, k ) into the equation from part (a).
(c) Recall that the formula for slope is
represented by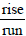 
. In the equation
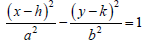, what is the “rise” of
each slant asymptote from the center? What
is the “run” of each slant asymptote from the
center?
(d) Based on the answers to part (c), what is the
slope of each of the asymptotes for the graph
of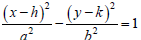 
? (Remember that
there are two slant asymptotes passing
through the center of the hyperbola, one
having positive slope and one having
negative slope.)
(e) Substitute the slopes from part (d) into the
equation from part (b) to obtain the
equations of the slant asymptotes.
19. In the standard form for the equation of a
hyperbola, a2 represents (choose one):
the larger denominator
the denominator of the first term
20. In the standard form for the equation of a
hyperbola, b2 represents (choose one):
the smaller denominator
the denominator of the second term
Answer the following for each hyperbola. For answers
involving radicals , give exact answers and then round
to the nearest tenth.
(a) Write the given equation in the standard form
for the equation of a hyperbola. (Some
equations may already be given in standard
form.)
It may be helpful to begin sketching the graph for
part (h) as a visual aid to answer the questions
below.
(b) State the coordinates of the center .
(c) State the coordinates of the vertices, and then
state the length of the transverse axis.
(d) State the coordinates of the endpoints of the
conjugate axis, and then state the length of the
conjugate axis.
(e) State the coordinates of the foci.
(f) State the equations of the asymptotes.
(Answers may be left in point-slope form.)
(g) State the eccentricity.
(h) Sketch a graph of the hyperbola which
includes the features from (b)-(f), along with
the central rectangle. Label the center C, the
vertices V1 and V2, and the foci F1 and F2.
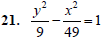
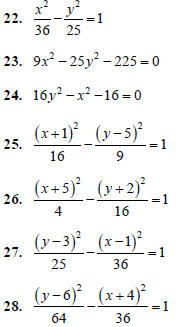
29. x2 − 25y2 + 8x −150y − 234 = 0
30. 4y2 −81x2 = −162x + 405
31. 64x2 − 9y2 +18y = 521−128x
32. 16x2 − 9y2 − 64x −18y −89 = 0
33. 5y2 − 4x2 − 50y − 24x + 69 = 0
34. 7x2 − 9y2 − 72y = 32 − 70x
35. x2 − 3y2 = 18x + 27
36. 4y2 − 21x2 −8y − 42x − 89 = 0
Use the given features of each of the following
hyperbolas to write an equation for the hyperbola in
standard form.
37. Center: (0, 0)
a = 8
b = 5
Horizontal Transverse Axis
38. Center: (0, 0)
a = 7
b = 3
Vertical Transverse Axis
39. Center: (−2, − 5)
a = 2
b =10
Vertical Transverse Axis
40. Center: (3, − 4)
a =1
b = 6
Horizontal Transverse Axis
41. Center: (−6,1)
Length of transverse axis: 10
Length of conjugate axis: 8
Vertical Transverse Axis
42. Center: (2, 5)
Length of transverse axis: 6
Length of conjugate axis: 14
Horizontal Transverse Axis
43. Foci: (0, 9) and (0, − 9)
Length of transverse axis: 6
44. Foci: (5, 0) and (−5, 0)
Length of conjugate axis: 4
45. Foci: (−2, 3) and (10, 3)
Length of conjugate axis: 10
46. Foci: (−3, 8) and (−3, − 6)
Length of transverse axis: 8
47. Vertices: (4, − 7) and (4, 9)
b = 4
48. Vertices: (1, 6) and (7, 6)
b = 7
49. Center: (5, 3)
One focus is at (5, 8)
One vertex is at (5, 6)
50. Center: (−3, − 4)
One focus is at (7, − 4)
One vertex is at (5, − 4)
51. Center: (−1, 2)
Vertex: (3, 2)
Equation of one asymptote:
7x − 4y = −15
52. Center: (−1, 2)
Vertex: (3, 2)
Equation of one asymptote:
6x + 5y = −7
53. Vertices: (−1, 4) and (7, 4)
e = 3
54. Vertices: (2, 6) and (2, −1)
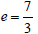
55. Center: (4, − 3)
One focus is at (4, 6)
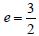
56. Center: (−1, − 2)
One focus is at (9, − 2)
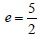
57. Foci: (3, 0) and (3, 8)
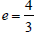
58. Foci: (−6, − 5) and (−6, 7)
e = 2
| Prev | Next |