Linear Algebra
Gaussian Elimination
1. Which of the following matrices is NOT row equivalent to the one below ? In
other
words, which matrix could you NOT get from the matrix below through elementary
row operations ?

a.
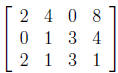
b.
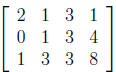
c.

(d) More than one of the above
(e) All are possible through elementary row operations.
2. Which of the following matrices is row equivalent to the one below? In other
words,
which matrix could you get from the matrix below through elementary row
operations?
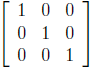
a.
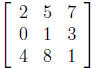
b.

c.
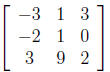
(d) More than one of the above
(e) All are possible through elementary row operations.
3. Which of the following matrices is NOT row equivalent to the one below? In
other
words, which matrix could you NOT get from the matrix below through elementary
row operations?

a.

b.
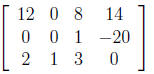
c.

(d) All are possible through elementary row operations.
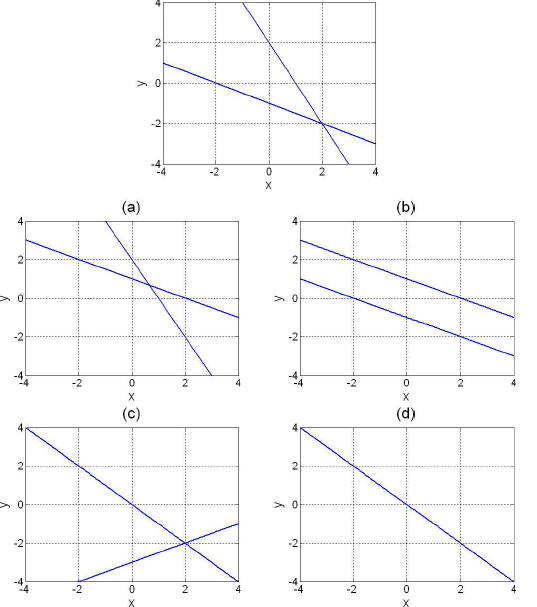
4. A linear system of equations is plotted below. We create an augmented matrix
to
represent this linear system , then perform a series of elementary row
operations. Which
of the following graphs could represent the result of these row operations?
5. We have a system of two linear equations and two
unknowns which we solve by per-
forming Gaussian elimination on an augmented matrix. Along the way we create the
graphs below, showing geometrical representations of the initial system, the
system at
an intermediate step in the row reduction process , and the system after it has
been
put into reduced row echelon form. Put these graphs in order , starting with the
initial
system and ending with the system in reduced row echelon form.
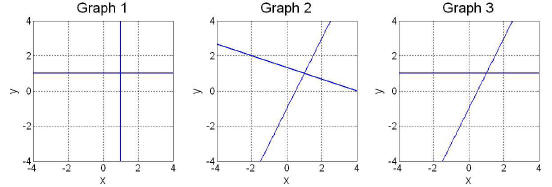
(a) Graph 2, Graph 3, Graph 1
(b) Graph 1, Graph 3, Graph 2
(c) Graph 1, Graph 2, Graph 3
(d) Graph 2, Graph 1, Graph 3
(e) Graph 3, Graph 2, Graph 1
6. What is the value of a so that the linear system represented by the following
matrix
would have infinitely many solutions ?
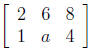
(a) a = 0
(b) a = 2
(c) a = 3
(d) a = 4
(e) This is not possible.
(f) More than one of the above
7. We start with a system of two linear equations in two variables and we
translate this
system into an augmented matrix M. After performing Gaussian elimination,
putting
this matrix into reduced row echelon form, we get the matrix R which tells us
that
this system has no solution. How could we geometrically represent the linear
equations
contained in the rows of the augmented matrix R?
(a) We can represent the equations of R as two parallel lines.
(b) We can represent the equations of R as two lines that may not be parallel.
(c) We can represent the equations of R as a single line.
(d) The equations of R cannot be represented geometrically.
8. We start with a system of three linear equations in three variables and we
translate
this system into an augmented matrix M. After performing Gaussian elimination,
putting this matrix into reduced row echelon form, we get the matrix R which
tells us
that this system has no solution. How could we best geometrically represent the
linear
equations contained in the rows of the augmented matrix M?
(a) We can represent the equations of M as three parallel lines.
(b) We can represent the equations of M as three parallel planes.
(c) We can represent the equations of M as three planes,
where at least two must be
parallel.
(d) We can represent the equations of M as three planes, where none of the
planes
ever intersects with another.
(e) We can represent the equations of M as three planes, which do not share any
points in common .
(f) The equations of M cannot be represented geometrically.
9. Howard's store sells three blends of our: standard, extra wheat, and extra
soy. Each
is a blend of whole wheat our and soy our, and the table below shows how many
pounds of each type of our is needed to make one pound of each blend.
| whole wheat our | soy our | |
| 0.5 | 0.5 | Standard Blend |
| 0.8 | 0.2 | Extra Wheat |
| 0.3 | 0.7 | Extra Soy |
A customer comes in who wants one pound of a blend that is
60% wheat and 40% soy.
We can solve the following system of equations to determine the amount of
Standard
Blend (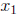 ), Extra Wheat Blend (
), Extra Wheat Blend (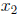 ),
and Extra Soy Blend (
),
and Extra Soy Blend (![]() )
needed to create this
)
needed to create this
special mixture.
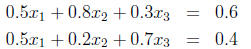
If we form an augmented matrix for this system, the
reduced row echelon form is
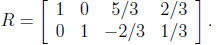
If the store is out of Extra Soy Blend, how much of each
of the other blends is needed?
(a) 2/3 pound of Standard Blend and 1/3 pound of Extra Wheat Blend
(b) 5/3 pound of Standard Blend and 2/3 pound of Extra Wheat Blend
(c) There are an infinite number of options for the amounts of Standard and
Extra
Wheat Blend.
(d) It is not possible to create this mixture without Extra Soy Blend.
10. Referring to the previous question , if the store is out of Extra Wheat Blend
(![]() ), how
), how
much of each of the other blends is needed to make the special mixture?
(a) 2/3 pound of Standard Blend and 1/3 pound of Extra Soy Blend
(b) 1/6 pound of Standard Blend and 1/2 pound of Extra Soy Blend
(c) There are an infinite number of options for the
amounts of Standard Blend and
Extra Wheat Blend.
(d) It is not possible to create this mixture without Extra Wheat Blend.
11. Referring to the previous two questions, what values are realistic for
![]() in this context?
in this context?
(a) 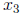 can be any value.
can be any value.
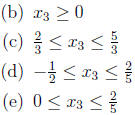
| Prev | Next |