Math 103-1 Final Exam Review Sheet

The final exam is comprehensive. It covers chapters 2, 3, 4, 5, 6, 7, and 8. Specific sections
and content is listed below. You may bring a simple scientific calculator, but no
graphing/symbolic/cell phone calculators are allowed . You may use a 5×7 inch hand
written note card. Don't be late.

Chapter 2: Linear Equations and Inequalities

x2.1: Linear Equations : Be able to solve linear equations. Be able to find the LCD in
case that there are fractions. Be able to check your answer.
x2.2: Linear Equations and Problem Solving: Be able to work with percentages
and proportions . Two shapes that are the same shape, but a different size are what?
x2.3: Business and Scientific Problems: Be able to set up and solve a simply rate
problems. I could ask a business, mixture, or distance problem. What is d = r×t? Know
the equations for a square, rectangle, circle , and triangle. Be able to solve given formulas
for another variable . Be able to do a word problem that deals with geometry.
x2.4: Linear Inequalities: Be able to solve linear inequalities of one variable. When
does the inequality change direction? Be able to state the answer using an inequality,
interval notation, and on a number line . Be able to solve compound equalities of the form
5 < 2x - 5 < 10 and of the form 2x > 1 or - 6 > 3x.
x2.5: Absolute Value Equations and Inequalities: Be able to solve basic absolute
value problems like|2x - 4 | + 3 = 6 and like| x + 5| = |x + 11|. Make sure and check your
answers because sometimes the ones you find won't work. Be able to solve absolute value
inequalities like |3x - 4|≥5 and |2 - 1/3x| ≤1/100. Be able to express your answers on a
number line, with interval notation, and with inequalities.

Chapter 3: Graphs and Functions

x3.1: The Rectangular Coordinate System : Be able to plot points (ordered pairs).
Be able to build tables from given equations, like lines . Be able to find the distance between
two given points. What is the Pythagorean Theorem? Be able to find the midpoint (average)
between two points.
x3.2: Graphs of Equations: Be able to graph a given function by building a table of
values and plotting those values. Be abe to find intercepts of equations, both x and y.
x3.3: Slope and Graphs of Linear Equations: Given two points, be able to find the
slope of the line that passes through them. What kind of lines have zero slope ? Vertical
(undefined) slope? Given the equation of a line, be able to find its slope. Know the slope-
intercept form of a line y = mx + b. What is m? What is b? When are two lines parallel?
Perpendicular? What is m₁ = -1=m₂ for? Note that slope represents the average rate of
change of a process .
x3.4: Equations of Lines: Be familiar with the point-slope form of a line y - y₁ =
m(x - x₁). What is m? What is (x₁; y₁)? Be familiar with the general form of a line
ax + by + c = 0. What is x = a? y = b?
x3.5 Graphs of Linear Inequalities: Be able to sketch the solutions of linear inequal-
ities.
x3.6 Relations and Functions: What is a relation? What is domain? What is range?
What is a function? Be familiar with function notation. Be able to evaluation functions at
a given number, a variable, a smiley face, a tree, or an expression . Be able to find both the
domain and range of a function. Be able to find the domain of functions like f(x) = x²-4x,

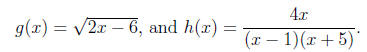
x7. Graphs of Functions: Be able to sketch a function. Be able to use a table of
values to sketch a graph. Be able to sketch piecewise functions. Be able to sketch functions
with a given domain. Be able to use the vertical line test to determine whether a graph is a
function or not (relation). Be familiar with shifts and reflections. Be familiar with the six
basic functions and their graphs.