Linear Mathematics Review 1
1. The straight line goes through the points (-3, 2) and
(4, -1). Find the slope of the line .
According to the formula 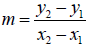 we have
we have
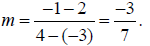
2. Write a point-slope equation for the line from Problem
1.
If we know the slope m and a point 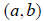 on the
straight line we can write an equation in the point-slope form as
on the
straight line we can write an equation in the point-slope form as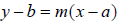 .
If we use e.g. the point (-3,2) then we can write
.
If we use e.g. the point (-3,2) then we can write
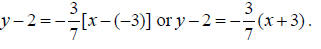
3. Write the slope- intercept equation for the line from
Problem 1.
We will solve the equation we got in the previous problem for y.
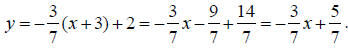
4. Write an equation of the line parallel to the line from
Problem 1 and going through the
point (1,3).
Parallel lines have equal slopes and therefore we can write an equation of this
parallel line in the point-slope form
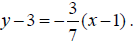 Solving for y we get an equation in the
slope- intercept form
Solving for y we get an equation in the
slope- intercept form 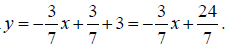
5. Write an equation of the line perpendicular to the line
from Problem 1 and going
through the point (1,3).
The slopes of perpendicular lines are negative reciprocals
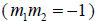 and therefore the slope of the perpendicular
line is 7/3 and its equation in the point-slope form
and therefore the slope of the perpendicular
line is 7/3 and its equation in the point-slope form
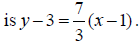 Solving for y we get an equation in the
slope-intercept form
Solving for y we get an equation in the
slope-intercept form 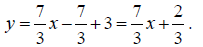
6. Graph the lines from Problems 1 and 5 in the same coordinate system.
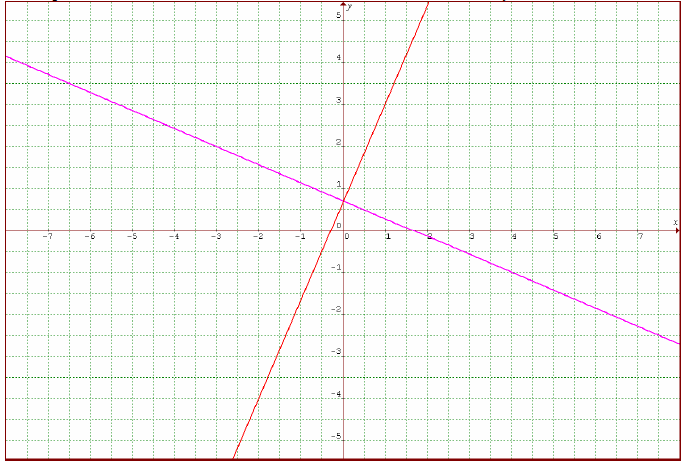
7. Find the point of intersection of the lines from
Problems 1 and 5.
We have to solve the system of equations
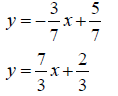
Because the left parts are equal so are the right parts.
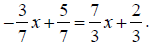 Multiplying both parts
by the common denominator , 21, we get
Multiplying both parts
by the common denominator , 21, we get
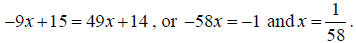 After we plug this value of x into the firs
equation we get
After we plug this value of x into the firs
equation we get 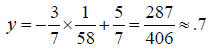
8. The straight line has the x-intercept -2 and the
y-intercept 3. Write an equation of the
line. We use the formula 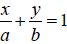 where a and b are
the x-intercept and the y-intercept, respectively. In our case
where a and b are
the x-intercept and the y-intercept, respectively. In our case
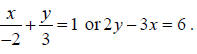
9. If the price of a CD-player is $40 the demand is 4000.
If the price of the same
CD- player is $60 the demand is 3000. Assuming that the demand is a linear
function
of the price find the demand if the price is $55.
First we need the slope-intercept equation of the line
through the points (40, 4000) and (60, 3000). The slope of the line is
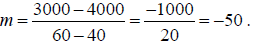 Using for example the first point we can
write an equation of the line in the point-slope
Using for example the first point we can
write an equation of the line in the point-slope
form 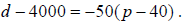 . From here,
. From here,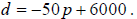 If then.
If then. 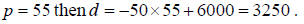
10. A small company produces dolls. The permanent monthly
expenses are $6000 and the
Cost of producing a doll is $3. If the dolls sell for $10 each what is the
breakeven
point?
The cost of producing x dolls is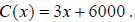 The corresponding revenue is
The corresponding revenue is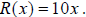 To find the
break-even point we have to solve the equation
To find the
break-even point we have to solve the equation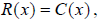 or
or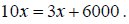 We have
We have 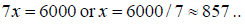
| Prev | Next |