Get it on Google Play Get it on Apple Store

MATH-120 Review Questions

1. Perform the indicated operation: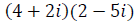

2. Write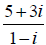 in the form

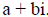
3. Find the exact distance between the points (3, -2) and (-1, 4).

4. Find the exact distance between the points (1,-6) and (-8,-4).

5. Find the solution set : 4x – (2x + 2) = 3(x – 2)

6. Find the solution set: 5x − (2x −10) = 35

7. Find the solution set:

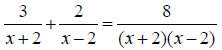
8. Find the solution set:

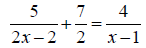
9. The formula P = 2L + 2W gives the perimeter of a rectangle with length (L) and width (W).
Solve for W .

10. The formula A= P + Prt gives the amount of money (A) you have when a principal amount
(P) is invested at a rate r for t years. Solve the formula for t.

11. Find the solution set: (3x −1)^2 =16

12. Find the solution set: (4x −12)^2 = 81

13. Find the solution set, giving exact solutions: 4x^2 − 2x +1 = 0

14. Find the solution set, giving exact solutions: 3x^2 − 2x + 4 = 0

15. Find the solution set:

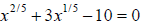
16. Find the solution set:

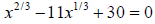
17. Find the solution set:

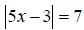
18. Find the solution set:

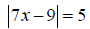
19. Solve the inequality, and then graph the solution :

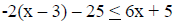
20. Solve the

inequality, and then graph the solution: −8(x −1) ≥ 32

21. Solve the inequality. Write your solution using interval notation: | x + 3 |> 2

22. The length of a rectangular garden is 3 feet greater than the width. The area is 108 square
feet. Find the length and width of the garden.

23. Solve the inequality. Write your solution using interval notation:

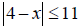
24. Solve the inequality. Write your solution using interval notation: | 2x +1|≤11

25. Solve the equation:

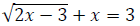
26. Solve the equation:

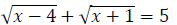
27. A ball is thrown upward from the ground. The height of the ball in feet above ground after t
seconds is given by the formula h = −16t^2 + 48t . During which time interval will the ball’s
height exceed 32 feet? What is the maximum height reached by the ball?

28. Solve the quadratic inequality and express the solution set in interval notation: x^2 − 4x + 3 > 0

29. Solve the rational inequality and express the solution set in interval notation:

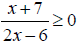
30. Solve the rational inequality and express the solution set in interval notation:

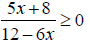
31. A new car that was worth 24 thousand dollars in 2002 ( x = 2 ) will be worth 13 thousand
dollars in 2006 ( x = 6). Assuming the depreciation is linear, find an equation for the
depreciation y in terms of x years .

32. Write an equation for the line passing through the points (1,-1) and (-1,4). Write your answer
in slope-intercept form.

33. Determine the slope and y -intercept of the graph of the equation11x + 2 y − 5 = 0 .

34. Determine the slope and y-intercept of the graph of the equation 9x − 8y = 72 .

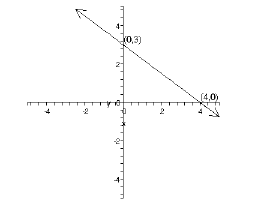
35. Give the equation of the line in slope-intercept form.

36. A line contains the point (4, 2) and is perpendicular to the line whose equation is y = 3x − 2 .
Give the equation for the line in slope-intercept form.

37. A solid line contains the point (3,2) and is perpendicular to the dotted line whose equation is
y=2x. Give the equation of the solid line in slope-intercept form.

38. Complete the squares as needed to put the equation of the circle in standard form. Give the
center and the radius of the circle.

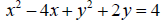
39. Give the center and radius of the circle with equation:

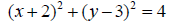
40. Find f(-2) for the piecewise function:

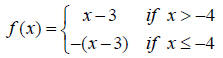
41. Find f(-6) for the piecewise function:

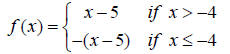
42. Give the domain of the function,

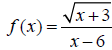
43. Give the domain of the function. Write the domain using interval notation:

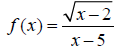
44. Find the domain and range of the function graphed. Write the domain and range using
interval notation.

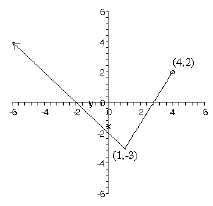
45. Identify 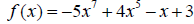is even, odd or neither.

46. Determine if 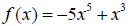is even, odd or neither.

47. Let 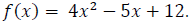Find and simplify the difference quotient

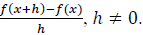
48. Let

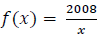
Find and simplify the difference quotient

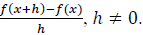
49. Here is the graph of y = f(x). On the same set of axes, graph g(x) = f(x – 3) – 2, labeling
the coordinates of the corresponding 4 points

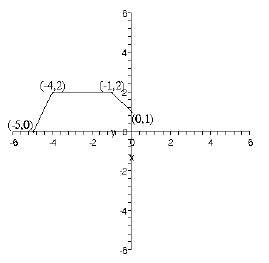
50. Consider the function f(x) whose graph appears in problem 49. Find the domain of f, the
range of f, the interval(s) on which f is increasing, the intervals on which f is decreasing,
and the intervals on which f is constant.

51. Consider the functions f (x) = x^2 + 2 and g(x) = 2x – 3. Find 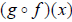. Simplify your
answer.

52. Consider the functions defined by f (x) = x^2 − 2 and g(x) = 3x − 4 . Find 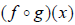. Simplify
your answer.

53. Consider the function defined by f (x) = 4x^3 + 2 . Find the inverse of the function f .

54. Consider the function defined by

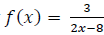
Find the inverse of f .

55. Here is the graph of a function f . Sketch the graph of f−1 on the same axes.

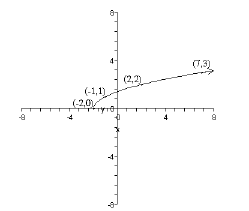
56. Find the coordinates of the vertex for the parabola defined by the function
f (x) = 4(x + 3)^2 − 7. Also find the axis of symmetry, find the x and y intercepts, and
sketch a graph of the parabola.

57. Find the coordinates of the vertex for the parabola defined by the function
f (x) = 4(x − 2)^2 − 9 . Also find the axis of symmetry, find the x and y intercepts, and
sketch a graph of the parabola.

58. Find the x-intercepts of the function defined by g(x) = 2(x − 6)(x + 5).

59. Find the x-intercepts of the function defined by g(x) = 3(x + 5)(x − 4)

Multiple Choice

60. Describe the end behavior of the function defined by f (x) = −5x^3 + ax^2 + bx + c , where a,
b, and c are real numbers .

A. falls to the left, falls to the right
B. falls to the left, rises to the right
C. rises to the left, rises to the right
D. rises to the left, falls to the right

Multiple Choice

61. Describe the end behavior of the function defined by

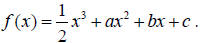
A. rises to the right, falls to the left
B. rises to the right, rises to the left
C. falls to the right, rises to the left
D. falls to the right, falls to the left

Multiple Choice

62. Consider the following graph:

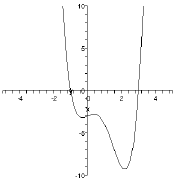
This is most likely the graph of which of the following functions? In the following
selections a, b, c, and d are real numbers .

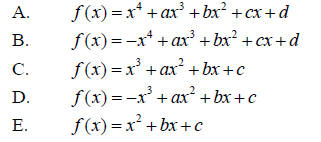
63. List all possible rational zeros of the polynomial function

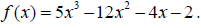
64. List all possible rational zeros of the polynomial function

65. Solve the polynomial equation 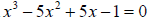Use synthetic division to find one root,
and then use this root to find all of the roots of the equation.

66. Solve the polynomial equation 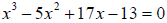Use synthetic division to find one
root, then use this root to find all of the roots of the equation.

67. Find the quotient and the remainder when x^3 − 2x^2 − 6 is divided by x – 3.

68. The width of a rectangular box is three times the height and the length is 8 inches more than
the height. If the volume is 120 cubic inches, find the dimensions of the box.

69. Given that i is a root of the equation 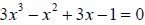find the solution set of the equation.

70. Given that i is a root of the following equation, find the solution set:

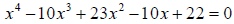
71. Find a third degree polynomial function f(x) with real coefficients such that -2, 1, and 5 are
zeros and f(2) = -24.

72. Find a third degree polynomial function with real coefficients such that 3 and i are zeros and
f(2) =10.

73. Solve the system of equations:

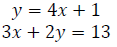
74. Solve the system of equations:

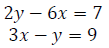
75. Solve the system of equations:

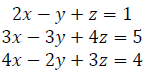
76. Find the quadratic function 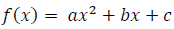whose graph goes through the points
(1,4), (3,20), and (-2,25).

77. Write the augmented matrix for the system of linear equations :

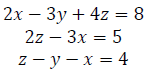
78. Write the augmented matrix for the system of linear equations:

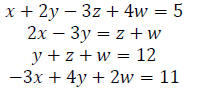
79. Perform the matrix row operation and write the new matrix: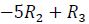

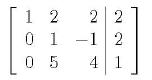
80. Perform each matrix row operation and write the new matrix: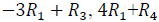

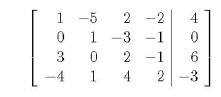
81. Answers
Note: The graphical solutions were omitted here.

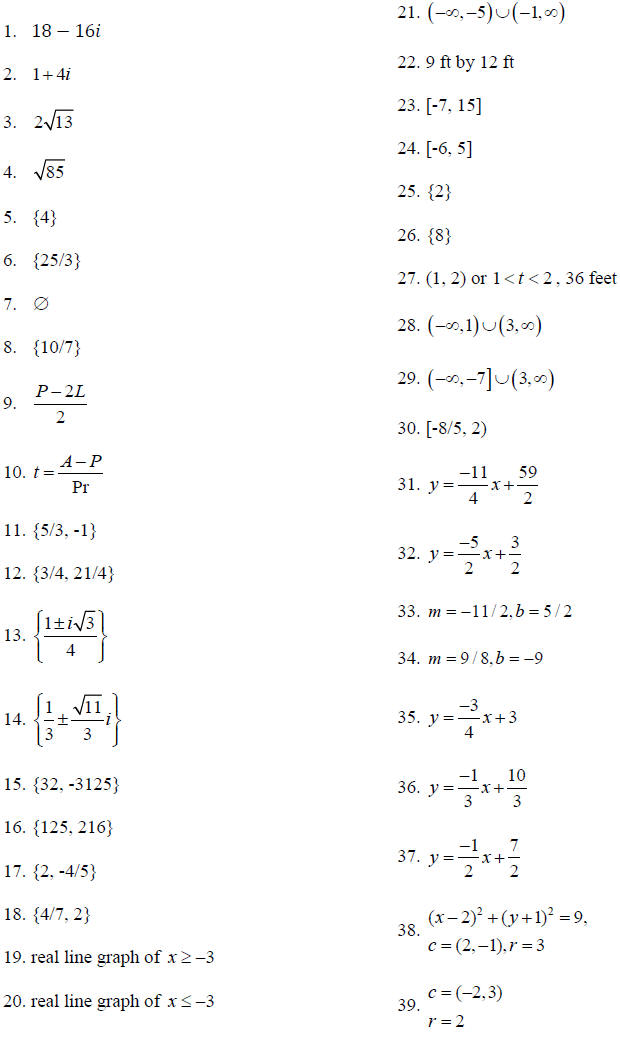
Prev Next