Math 171 Review for the Final Exam Solutions
5. Find the values of a and b , if the tangent line to y =
ax2 - bx at
(-2, 5) has slope m = 2. (5 points)
Solution. Because y(-2) = 5 we have the following equation for a
and b.
4a + 2b = 5
The derivative ![]() is 2ax - b. Because
is 2ax - b. Because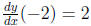 we have the second
we have the second
equation for a and b .
-4a - b = 2.
Adding the equations we get
b = 7
and plugging this value of b into the first equation we get 4a + 14 = 5
whence
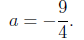
6. If a ball is thrown vertically upward with a velocity of 80 ft/s, then its
height after t seconds is h(t) = 80t - 16t2. What is the velocity of the
ball when it is 96 ft above the ground on its way up? On its way
down? (5 points)
Solution The velocity of the ball equals to the derivative of its height.
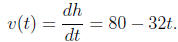
We can find the moments of time when the ball is 96 ft high
by
solving the quadratic equation
80t - 16t2 = 96.
Dividing both parts by -16 and moving all terms to the left we get
t2 - 5t + 6 = 0
whence t = 2 or t = 3. At the moment t = 2 the velocity of the ball is
16 ft/sec and the ball is moving up whilst at the moment t = 3 the
velocity is -16 ft/sec and the ball is moving down.
7. An open box is to be made from a 6ft by 8ft rectangular piece of
sheet metal by cutting out squares of equal size from the four corners
and bending up the sides. Find the maximum value that the volume
of the box can have.(10 points)
Solution Let x be the side of each cut out square. Then the height of
the box is x
whilst its length is 8-2x and its width is 6-2x (See the picture below).
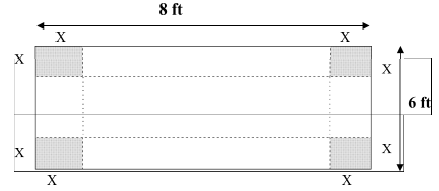
Notice that because these dimensions cannot be negative we
have
0 ≤ x ≤ 3. There fore we have to maximize the volume of the box
V (x) = x(8-2x)(6-2x) = 4x(4-x)(3-x) = 4x(x2-7x+12) = 4(x3-7x2+12x)
on the interval [0, 3]. At the ends of the interval the function V takes
value 0 so it will take the greatest value at a stationary point inside
the interval. To find the stationary points we have to solve the
equation
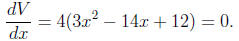
The quadratic formula provides two solutions
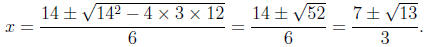
The sign + provides a solution which is greater than 3 and
of no
interest to us. The only stationary point inside the interval [0, 3] is
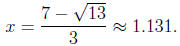
You can easily check yourself that the greatest value of the volume is
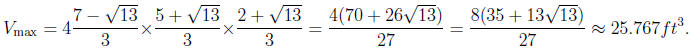
8. Sketch the graph of y = x3 - 3x + 2. Find x- and y-
intercepts, plot
the stationary points and the inflection points and determine the
intervals where y is increasing and decreasing, concave up and
concave down.(10 points)
Solution. To find the x-intercepts we have to solve the equation
x3 - 3x + 2 = 0.
Notice that x = 1 is a solution of this equation and therefore x - 1 is
a factor of x 3 - 3x + 2. We can factor x3 - 3x + 2 using long division,
grouping , or synthetic division. The table below shows synthetic
division.
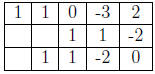
Therefore x3 - 3x + 2 = (x - 1)(x2 + x - 2) = (x - 1)2(x +
2) and the
x- intercepts are (-2, 0) and (1, 0).
The y-intercept is (0, 2).
The first derivative of y is
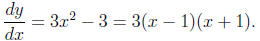
The function has two stationary points, -1 and 1 which
divide the
x-axis into the intervals (-∞,-1), (-1, 1), and (1,∞). The next
table shows the behavior of the function on these intervals.
| Interval | (-∞,-1) | (-1, 1) | (1,∞) |
| Sign of
|
+ | - | + |
| Behavior of y | Increases |
Decreases |
Increases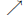 |
To find the inflection points of the cubic function y we
compute its
second derivative
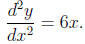
We see that y has only one inflection point 0. The
information about
concavity of y is contained in the next table.
| Interval | (-1, 0) | (0,1) |
| Sign of
|
- | + |
| Concavity | Down | Up |
A computer generated graph of the function y = x3 - 3x + 2
is shown
below.
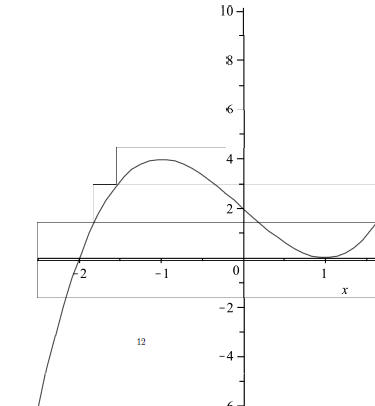
9. Use the fundamental theorem of calculus:(4 points each)
(a) Find the derivative of the function
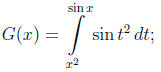
Solution. The fundamental theorem of calculus in its
generalized form tells us that
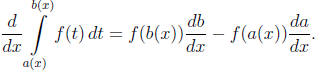
Applying this formula when a(x) = x2, b(x) = sin x, and
f(t) = sin t2 we get
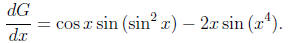
(b) Prove that the function
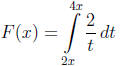
is a constant on the interval (-∞, 0).
Solution. Look at two ways to solve the problem.
First way. We apply the fundamental theorem of calculus to see
that
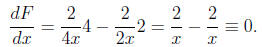
Because the derivative of F is identically 0 the function
F is a
constant function.
Second way.
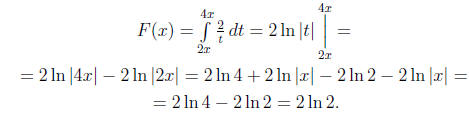
| Prev | Next |