MATH 385 HANDOUT 6

The final unit of the term covers fractions in depth , and some related topics.
Again, we’ll have you sign up for small groups to work on each problem. The
problems will be presented on Monday December 1 and Monday December 8.
For each project, your group must choose five problems from Chapter 5 that
relate to the themes of this project and solve them . Work them into the presentation
if appropriate.

For days when you are not presenting, you should work on the other questions
on the handout, prepare book problems related to those, go into greater depth in
a direction suggested by the problems, do outside research, or any combination of
these.

(1) (Return to Egypt)

Our “vulgar” fraction 3/5 can be written as the Egyptian fraction .
Think about the practical problem of trying to share three loaves of bread
between five people. How does each suggestion suggest that you might
divide the loaves? Draw this with rectangles to represent the loaves. Which
is more likely to seem fair? Try this again with the fractions12/13 and 5/8.

Another use of Egyptian fractions is for comparing fractions. If you
were teaching in school today,how would you teach students to compare
two fractions? Which is bigger, 4/7 or 5/8 ? How about 3/11 or 2/7? Could you
tell from looking at them, without doing a calculation? Now try writing
them as Egyptian fractions using the greedy algorithm. Does this make it
easier to compare them?

Look at the examples I gave you to test out in this problem. Are they
“rigged” to make a point, or do these methods always work this well?
Verify that


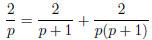
is always true. Explain why this is useful to find an Egyptian fraction
representation for 2/p when p is a prime greater than three.
Now consider the equation


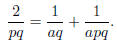
Solve for a in terms of p and q. How can you use this to help find Egyptian
fractions?

(2) (Five to the Pi)

We all know that the rule for exponents is that


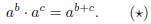
Explain why this is true when
a, b, c are natural numbers. We’ll treat the rest of the real numbers
( negatives , zero, fractions, and irrationals) as extensions of the natural
numbers, so the rule (*) should still be true: if a or b changes just a little
bit, then ab should also change just a little bit. (This is called continuity.)
Use the rule (*) to explain why


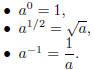
Explain the meaning of raising a number to an irrational power : what
is the meaning of ?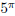

(3) (Rationals, Irrationals, Denseness)

The rational numbers are dense in the number line : this means that
between every two rational numbers, there is another rational. One consequence
of that is that even irrational numbers like 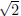can be approximated
as close as you like with rationals (even though you’ll never hit them exactly).

If someone gives you two rational numbers, explain how to find another
rational number in between them. Now explain why this means that there
are infinitely many rational values in between the numbers you started with.
Next, here is the outline of a proof that 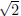is not a rational number.
Explain it to the class.


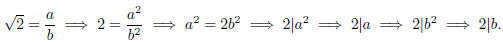
But this means that every fraction that represents 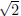is not in
lowest terms . This is impossible, so there must be no fraction that
represents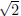

A good way to make sure you understand this proof is to modify it to
make a proof that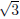 is irrational.

(4) (Lowest terms/“Simplest form”)

In this problem, a, b, c, d are assumed to be natural numbers.

Do several examples of putting a rational number in lowest terms and
putting a sum of two rational numbers in lowest terms.

Given a fraction a/b, explain how to put it in lowest terms. What are
the numerator and denominator of the answer? You should express this in
terms of a, b, their lcm, and their gcd.

Now suppose a/b and c/d are already in lowest terms. Put the sum
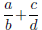
in lowest terms. What are the numerator and denominator of the answer?
You should express this in terms of the variables and whichever lcm and
gcd terms you need.

(5) ( Converting fractions to decimals)

First, explain how to convert a fraction
to a decimal, and a terminating decimal into a fraction .
• From looking at a rational number, how can you tell whether the
decimal expansion will be terminating or repeating?
• Which fraction is 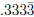? How about 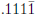and 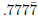? How about
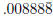? And 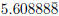? What about 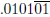? Explain how to convert
a repeating decimal into a fraction.
• The word “decimal” applies to base 10. (The root deca - means ten,
like in decade, decathlon, and decagon.) What is 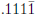in base 2? How
about in base 4?

(6) (Fractions within fractions)

Consider the funny- looking expression


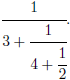
Simplify it to a fraction. Try this with a few other examples in the place
of 3, 4, and 2.

Now try this bunch of numbers:
 

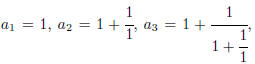
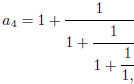
and so on.
What do you get for these values? What is the recursive formula for an ?
What is the pattern?

Find a way to quickly generate the an on a calculator, and find the value
of an for a large value of n.

Challenge problem: Given a rational number, find a way to write it as a
nested fraction like the ones above. Good ones to start with:
73/21 and 22/9.

What does this have to do with the Euclidean algorithm?