Math 74 Schedule
Here is an outline/summary of what we will cover/what we have covered on each
day.
This schedule serves at least three purposes. First, it gives me an idea of how
to pace the
class in order to cover all the material, and second, it allows the students to
estimate what
will be covered to prepare ahead of time, and third, if a student must miss
class, it will allow
them to see what they have missed.
1 Statements, Implications, and Logical Connectives
Class 1 (August 28).
introduction
statements
truth value
truth tables
implications (P -> Q)
inverse, converse, and contrapositive
the logical connectives “and”
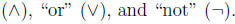
2 Sets
Class 2 (September 2).
sets, elements of sets (∈)
empty set (Φ)
containment
,
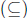subsets, equality of sets
operations on sets : union
,
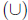intersection
,
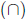complement ( difference ) (X \ Y ,
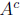for
),
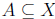(Cartesian) product (X × Y )
disjoint sets (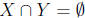
)
proper subsets
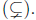
power set (P(X)).
Class 3 (September 4).
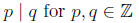
quantifiers: for all
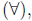there exists
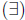
negation of quantifiers
statements that rely on sets, proving statements that rely on sets
the following statements are equivalent :
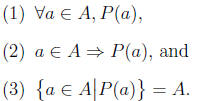
3 Relations
Class 4 (September 9).
relations (R)
reflexive, symmetric, antisymmetric, transitive, and skew-transitive relations
equivalence relations
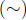
partial orders
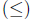
4 Induction, Strong Induction, and the Well Ordering Principle
Class 5 (September 11).
statements depending on
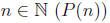
induction
strong induction
Class 6 (September 16).
the well ordering principle
prime numbers
the equivalence of induction, strong induction, and the well ordering principle
5 Functions
Class 7 (September 18).
domain, codomain, rule definition of a function
image
injective, surjective, and bijective functions
graph
graph defintion of a function
equality of functions
composition of functions, associativity of function composition
Class 8 (September 23). Review for Exam 1.
Class 9 (September 25). Exam 1.
Class 10 (September 30).
image and preimage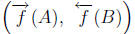
restriction and corestriction of functions
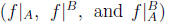
6 Invertible Functions
Class 11 (October 2).
invertible functions
left, right, and two sided inverses
theorem relating (left, right, two sided) inverses with (injective, surjective,
bijective) functions
axiom of choice
the set [n] for
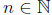
the injections
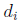and the surjections
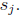
7 Cardinality
Class 12 (October 7).
the pigeonhole principle
finite sets, cardinality (#X = n)
infinite sets
countable sets
denumerable sets, cardinality
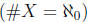
uncountable sets
Class 13 (October 9).
the subset/cardinality lemma
a set is countable <-> it is finite or denumerable
reconciling two definitions of cardinality (for countable sets) (#X and |X|).
Class 14 (October 14).
the product of two denumerable sets is denumerable
Q is countable
R is uncountable
sets of functions
cardinality of such sets
relatively prime integers
8 Groups
Class 15 (October 16).
binary operations
magmas: associative, commutative, (left, right) cancellative
(left, right) identities and inverses
unital magmas, semigroups, monoids, (commutative) groups
Class 16 (October 21).
the group S n
equivalence classes
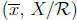
congruence modulo
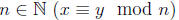
the group Z/n
more examples of groups
Class 17 (October 23).
more examples of groups
subgroups
group homomorphisms
definition of a ring, field
definition of a ring homomorphism
Class 18 (October 28). Review for Exam 2.
Class 19 (October 30). Exam 2.
9 Examples of Rings and Fields
Class 20 (November 4).
definition of a ring R and a field k
the rings Z, Z/n, Mn(R)
Class 21 (November 6).
the set of divisors D (n)
greatest common divisors (gcd(m, n))
the division theorem
the set of all primes is denumerable
Z/n is a field if and only if n is prime.
10 Metric Spaces
Class 22 (November 13).
metrics (distance)
metric spaces (X, d)
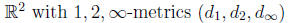
open ball at x of radius r (Br(x))
open, closed sets
Class 23 (November 18).
arbitrary union [intersection] of open [closed] sets is open [closed]
finite intersection [union] of open [closed] sets is open [closed]
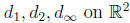give the same open sets
Class 24 (November 20).
sequences (xn)
convergent and Cauchy sequences
convergent implies Cauchy
completeness
limit points, set of limit points
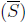
Class 25 (November 25).
a set S is closed if and only if
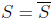
every convergent sequence is bounded
three definitions of a continuous function:
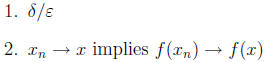
3. preimage of open sets are open
11 Complex Numbers
Class 26 (December 2).
complex numbers
the unit circle (S1)
S1 is a group
series
Euler’ s Formula
polar coordinates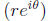 
Class 27 (December 4).
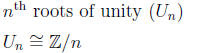
Class 28 (December 9).
Review for Final Exam.
| Prev | Next |