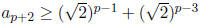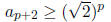Math Exam #2 ANSWERS
Write all answers legibly on the paper provided. If you
need extra paper, raise your hand and request a
blank paper – you must put your name on and hand-in any paper you receive. You
can also use the back
of the last page which is blank. Clearly label any answers that appear on a
paper different from where
the question appears. You must indicate the continuation of the answer on the
paper where the question
is and on the paper where the answer is continued. The number of points possible
for each question is
indicated in square brackets – the total number of points on the exam is 100,
and you will have exactly
1.25 hours to complete this exam. In order to receive any partial credit, you
must show your work, clearly
labled in the space provided. You may not use calculators , textbooks or any
other external aids during
this exam. The formula sheet is attached - this can be removed from the back of
the exam and does not
need to be handed in at the end.
Write the following University approved honor pledge and
sign on the blank provided after you complete
the exam. This must be done before we make the “stop writing now announcement.
I pledge on my honor that I have not given or received any unauthorized assistance on this examination.
____________________________________________________________________________________________________
____________________________________________________________________________________________________
____________________________________________________________________________________________________
Sign Here: ________________________
**** This area is for grading purposes (points lost per page)- Do not write below this line ****
1. [24 pnts.] Assume there are 25 balls in an Urn. 9 of
them are red, 6 are blue, 1 is yellow,5 are green
and 4 are purple.
Answer the following questions about those balls - You
must assume for all parts of this question that
balls of the same color are indistinguishable from each other. You do not have
to do the arithmetic , but
you do have to get each answer into a form that includes ONLY addition,
subtraction, multiplication ,
division, factorials and/or exponents : (Be sure to clearly label each of your
answers.)
a. [3 pnts.]If you were to draw all of the balls out of
the urn one at a time placing them on the
table in a straight line, how many different ways could that line look when you
are done?
ANSWER:
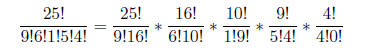
b. [3 pnts.] Assume one ball of each color fell off the
table, and you were able to find 3 of them.
How many different combinations of 3 balls might you have in your hand? (Assume
the order
you found the balls should not be considered here.)
ANSWER:
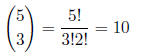
c. [3 pnts.] This question is the same as part b with the
one exception that this time you need to
consider the order you found the three balls.
ANSWER:
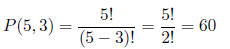
d. [3 pnts.] Assume the original 25 balls are back in the
urn. You draw two balls out at the same
time (there is no order between them). How many different combinations of 2
balls could you
have in your hand?
ANSWER:
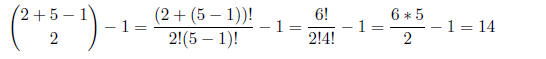
e. [4 pnts.]Assume the original 25 balls are back in the
urn. You draw two balls out at the same
time (there is no order between them). What is the probability that you get two
red ones?
ANSWER:
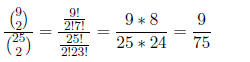
f. [4 pnts.] Assume the original 25 balls are back in the
urn. You draw six balls from the urn at
the same time (there is no order between them). What is the probability that you
do NOT have
a set of balls that are all the same color in your hand??
ANSWER:
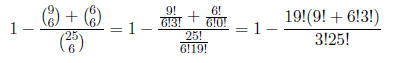
g. [4 pnts.]Assume the original 25 balls are back in the
urn. You draw one ball from the urn and
place it back into the urn, but remember what color it was. You then draw a
single ball from the
urn. What is the probability that the second ball drawn was the same color as
you remember
the first ball was?
ANSWER:
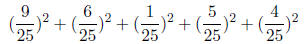
2. [23 pnts.] For each of the parts of this question:
Either give a counter example to dispove (giving
specific members for the sets A, B, C, D and U(universal) as needed and
justification as to why it is
a valid counter example) or prove the following statements concerning Sets.
Be sure to give the name of the reason which justifies each step you give in the
proof.
a. [7 pnts.]
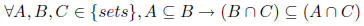
ANSWER: FALSE
Counter Example: A = {1},B = {1}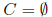
Since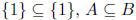 
so the
antecedent is true.
But
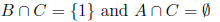
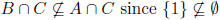so the consequent is
false
Since the antecedent is true and the consequent is false,
the implication is false and this is
a valid counter example.
b. [16 pnts.]
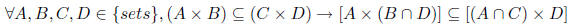
ANSWSER: True
Proof:
3. [14 pnts. - 2 each] For each of the following give the
set requested or the size of the set requested.
Assume ; indicates the empty set and U indicates the universal set.
When the answer is a number, you may leave it in the form that has ONLY
addition, subtraction,
multiplication, division and exponents . (NOTE: NOT FACTORIAL)
Assume P(M) indicates the Powerset of the set M.
Also assume n(M) indicates the size of the set M.
Assume that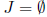 
; and K = {1, 2} and L = {1, 3}
Also assume n(W) = 100 and n(Y ) = 501 and n(V ) = 50
Z is the set of all integers.
4. [39 pnts.] For both of the parts of this question:
Either find a specific counter example or prove each
of the following statements is true. When using induction to prove something
true, you must only
use strong induction if it is required by that problem – using strong induction
to prove something
that only required regular induction, will result in a loss of points.
a. [18 pnts.]Prove or give a counter-example to the following:
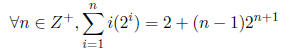
b. [21 pnts.] Using the fact that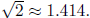
Assume the recurrence relation:
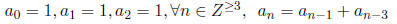
Prove or give a counter-example to the following:
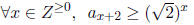
ANSWER:
| Base Case:(n = 0, n = 1, n = 2)
|
Inductive Hypothesis: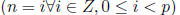
|
| Inductive Step:(n = p) Show:
|
| Proof: PART 1: (Find the Between value)
Since p−1 < p and p−3 < p because we are
subtracting a positive integer from the smaller and since p − 1≥0 and p − 3≥0 because the smallest
value of p is 3,
therefore let PART 2: (prove that it is an actual Between value) proof:
This is a contradiction since
and from part 1 we know
And so by the transitive property of ≥ we know:
QED |
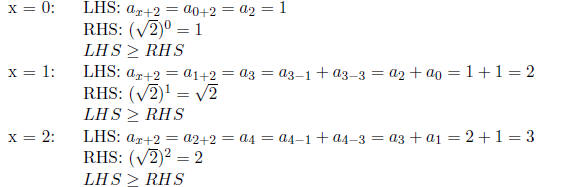
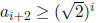
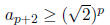
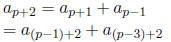
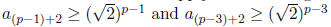by the IH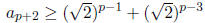
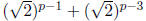be that between value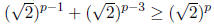
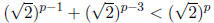
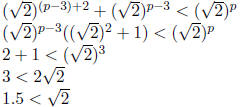
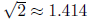
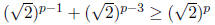by closing the
conditional world with a contradiction
| Prev | Next |