Model Answers for Test 2 with gr
Model Answers for Test 2 with grading scheme
#1: (a) Let G and H be groups . A map f: G->H is called an
isomorphism, if
a) f is a bijection
b) f(x*y)=f(x)*f(y) for all x and y in G (5p)
(b) a permutation is odd, if it can be written as a product of an odd number of
2-
cycles (5)
#2: Prove: If the identity permutation є is written as a
product of n transposition , then
n is even
Proof by induction: Assume that the statement is true for any r<n.
Now suppose that є=β1. . .βn, .where all βi are
2-cycles. Write βn as (ab). Then there
are four possibilities for βn-1βn:
o (ab)(ab) = є
o (ac)(ab) = (abc) = (ab)(bc)
o (bc)(ab) = (acb) = (ac)(bc)
o (cd)(ab) = (ab)(cd)
In the first case, βn-1βn cancels, and we can rewrite β1. . .βn
as β1. . .βn-2. By induction n-2
is even, and therefore n is even.z
In all other cases, we exchange the left side with the right side. This moves
the first
occurrence of the element a to the left. We continue to use the identities above
to move a
to the left. Eventually the first case has to happen, because if it would not,
then eventually
a would occur only in the left most transposition. But then the product of all
cycles
cannot be the identity, as a would not be mapped to itself.
#3. Suppose 3 is a generator of U(50). Find all other
generators.
Calculate all powers of 3 in U(50):
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 3 | 9 | 27 | 31 | 43 | 29 | 37 | 11 | 33 | 49 | 47 | 41 | 23 | 19 | 7 | 21 | 13 | 39 | 7 | 1 |
By the generator theorem, exactly those powers define
generators that are relatively
prime to 20: the powers 1, 3, 7, 9, 11, 13, 17, 19. (6)
the element 3 raised to those powers correspond to these elements in U(50):
3, 27, 37, 33,
47, 23, 13 (4)
#4. Suppose that f: U(50)->U(25) is an isomorphism, such
that f(3)=2.
(a) Use the homomorphism property of f to determine f(9) and f(27)
f(9)=f(3*3)=f(3)*f(3)=2*2=4
f(27)=f(33)=f(3)3=23=8
(b) What would f(7) have to be?
f(7)=f(315)=f(3)15=215=18
#5: List all elements of order 12 in Z240.
The first element of order 12 in Z240 is a=20. It generates the subgroup of
order 12:
<20>={0 20,40, 60, 80, 100, 120, 140, 160, 180, 200, 220} (4)
All other generators of this subgroup have also order 12. (2)
They are those multiples (1,5,7,11) of a=20 that are relatively prime to 12. (2)
So they are 20, 100, 140 and 220. (2)
#6: Consider the permutations alpha=(2345) and
beta=(123456) in S6.
(a) alpha-1=(5432)
(b) alpha=(23)(34)(45)
(c) alpha*beta=(1356)(24)
beta*alpha=(1246)(35)
(d) both have order 4
#7: Write down an
(a) even permutation of odd order: (123) (2)
(b) even permutation of even order: (12)(34) (4)
(c) odd permutation of even order: (1234) (2)
(d) odd permutation of odd order: impossible. (2)
(reason: if a permutation is written as a product of disjoint cycles, the order
is
the lcm of the length of the individual cycles. If the lcm is odd, that means
that
the length of each cycle is odd. But that means that each cycle is an even
permutation, hence the product must also be even) (5p ex cr)
#8: How many permutations of order 4 are there in S4?
There is one type of permutation of order 4:
(1234) type: there are 4*3*2*1 divided by 4 of those , i.e., 6 total (5)
#9: Three things to check
(a) one-to-one: easy
(b)onto: easy (1)
(c) homomorphism property : (9)
f((a+ib)*(c+id)) =f(ac-bd+i(bc+ad))
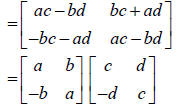
=f(a+ib) * f(c+id)
#10: Is U(64) cyclic?
No. There are several reasons one can give. One is that
<31>={1,31} and
<33>={1,33} are two different subgroups of the same order.
This can’t happen in a cyclic group . (10)
| Prev | Next |