noname
Abstract
The p-adic arithmetic allows error-free representation of fractions and
error -free arithmetic
using fractions. In this tutorial, we describe infinite- precision p -adic
arithmetic which is more
suitable for software implementations and finite-precision p-adic arithmetic
which is more suitable
for hardware implementations. The finite-precision p-adic representation is also
called
Hensel code which has certain interesting properties and some open problems for
research.
1 Introduction
A p- adic number α can be uniquely written in the form
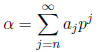
where each of 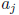 ∈ [0, p
− 1] and the p-adic norm of the number α is defined as
∈ [0, p
− 1] and the p-adic norm of the number α is defined as
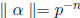 . Note
. Note
that the series
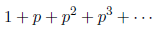
converges to 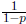 in the p-adic
norm. Now, as an example, consider the power series expansion
in the p-adic
norm. Now, as an example, consider the power series expansion
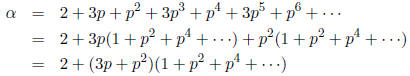
Since 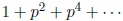 converges to
converges to
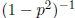 , we have
, we have
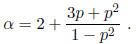
Taking p = 5, we obtain 5-adic expansion of
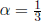 , which can be written in the form
, which can be written in the form
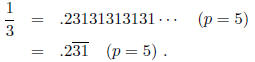
There is a one-to-one correspondence between the power series expansion
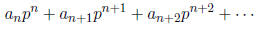
and the short representation
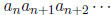 , where only the coefficients of the powers
of p are
, where only the coefficients of the powers
of p are
shown. We can use the p-adic point as a device for displaying the sign of n .
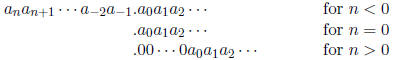
For example,
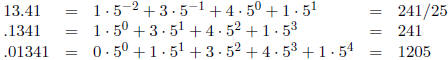
2 Representation of Negative Numbers
If
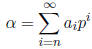
then
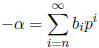
where 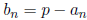 and
and
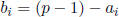 for i > n. Thus, for example,
for i > n. Thus, for example,
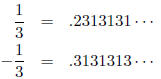
However, watch for leading zeros , they remain unchanged:
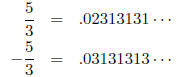
3 Representation of Integers
Since a positive integer h can be expressed in exactly one way as the sum of
powers of a prime p,
i.e.,
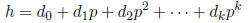
with 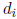 ∈ [0, p − 1],
there is essentially no difference between p-adic and p-ary representation of h.
∈ [0, p − 1],
there is essentially no difference between p-adic and p-ary representation of h.
The only difference is that the digits in the p -adic representation are written
in reverse order . For
example,
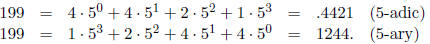
4 Representation of Rational Numbers
If α is a rational number , then it has a repeating pattern of
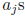 in its p-adic expansion, i.e., it is
of
in its p-adic expansion, i.e., it is
of
the form
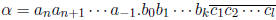
For example, 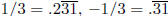 , and
, and
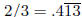 , etc. Let α have the p-adic expansion
, etc. Let α have the p-adic expansion
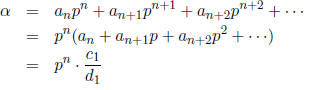
where 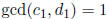 and p divides
neither
and p divides
neither 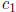 nor
nor
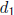 . The p-adic expansion for
. The p-adic expansion for
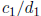 is
is
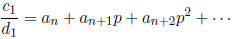
and thus
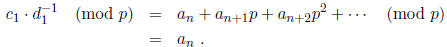
In other words, we compute
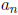 by
by
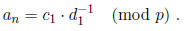
Next, we use
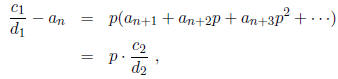
where 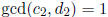 and p divides
neither
and p divides
neither 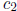 nor
nor
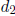 . The p-adic expansion for
. The p-adic expansion for
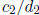 is
is
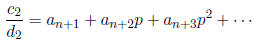
and so
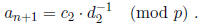
We continue this process until the period is exhibited. Let α = 2/15 and p = 5. Thus,
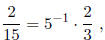
and n = -1. The 5-adic expansion of 2/15 is found as
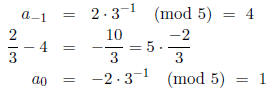
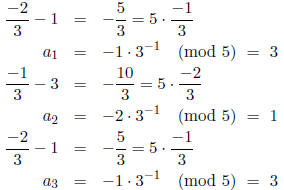
which gives us 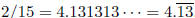 .
.
| Prev | Next |