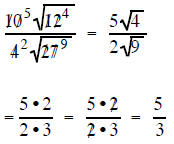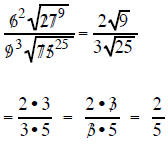Rationalizing the Denominator of a Fraction
Rationalizing the Denominator of a Fraction
with a Monomial Term that Contains a Square Root
Each of following factions has a monomial expression in the
denominator that
contains a square
root or a square root multiplied by a number.

It is common to require that the denominator of a fraction not contain any
radicals. The process of
eliminating radicals from the denominator of a fraction is called rationalizing
the denominator.
Reducing Factions with Monomial terms like sqrt(A)/sqrt(B)
Many fractions with square roots in both the numerator and denominator can be
simplified by reducing
the numbers under the square roots. Fractions with only monomial terms that are
each under a square
root like sqrt(A)/sqrt(B) may be reduced if A and B have a common factor. If the numbers under the square
roots have a common factor then the numbers under the square roots can reduce
each other.
| Example 1 Simplify sqrt (12)/sqrt(3) |
Example 2 Simplify sqrt(50)/sqrt(8) |
| sqrt(12)/sqrt(3) the 12 and 3 are both factors under a radicalsign so they can reduce each other | sqrt(50)/sqrt(8) the 50 and 8 are both factors under a radical sign so they can reduce each other |
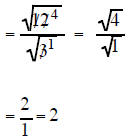 |
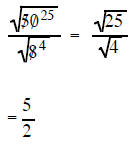 |
Reducing Factions with Monomial terms like 
Fractions with only monomial terms like 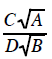 may be be reduced. If A and B have a common
may be be reduced. If A and B have a common
factor then the numbers under the square root can reduce each other. If C and
D
have a common
factor then the numbers outside the square root can reduce each other.
Warning: A number under a square root and a number outside a square root
CAN NOT
reduce
each other
| Example 3 Simplify 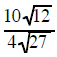 |
Example 4 Simplify 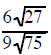 |
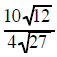 the 12 and 27 are both factors under a radical sign so they can reduce each other the 10 and 4 are both factors
outside a radical |
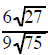 the 27 and 75 are both factors under a radical sign so they can reduce each other the 6 and 9 are both factors
outside a radical
|
|
|
|
Rationalizing the Denominator of a Fraction with
a Monomial Term that contains a Square Root
Many fractions with square roots can not be simplified by reducing the numbers
under the square
roots as in the examples above.

It is common to require that the denominator not contain any radicals. In
fractions where the numbers
under the square square roots cannot be reduced to eliminate the square root in
the denominator we
must find another process that will eliminate the radical from the denominator.
The process of
eliminating the radical from the denominator of a fraction is called
rationalizing the denominator.
Multiplying the fraction sqrt(A)/sqrt(B) by sqrt(B)/sqrt(B) will eliminate the radical from the denominator
| (7)/sqrt(3) multiply the top and bottom by sqrt(3) | (5)/sqrt(6) multiply the top and bottom by sqrt(6) |
| Example 5 Simplify (7)/sqrt(3) |
Example 6 Simplify (5)/sqrt(6) |
| (7)/sqrt(3) multiply the top and bottom by sqrt(3) | (5)/sqrt(6) multiply the top and bottom by sqrt(6) |
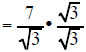 the sqrt(3) times
itself is 3 the sqrt(3) times
itself is 3 |
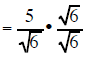 the sqrt(6) times
itself is 6 the sqrt(6) times
itself is 6 |
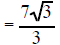 |
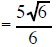 |
| Note: The 3 under the radical sign and the 3 outside the radical cannot reduce each other |
Note: The 6 under the radical sign and the 6 outside the radical cannot reduce each other |
| Example 7 Simplify (6)/sqrt(10) |
Example 8 Simplify (25)/sqrt(15) |
| (6)/sqrt(10) multiply the top and bottom by sqrt(10) | (25)/sqrt(15) multiply the top and bottom sqrt(15) |
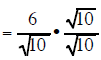 the sqrt(10) times
itself is 10 the sqrt(10) times
itself is 10 |
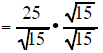 the sqrt(15) times
itself is 15 the sqrt(15) times
itself is 15 |
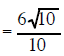 the 6 and 10 are both factors outside a radical sign so they can reduce each other |
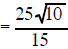 the 25 and 15 are both factors outside a radical sign so they can reduce each other |
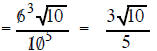 |
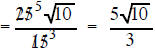 |
| Example 9 Simplify 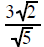 |
Example 10 Simplify 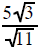 |
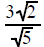 multiply the
top and bottom by multiply the
top and bottom by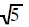 |
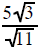 multiply the
top and bottom by multiply the
top and bottom by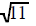 |
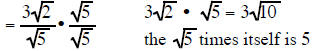 |
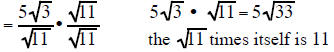 |
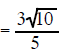 |
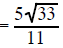 |
| Example 13 Simplify  |
Example 14 Simplify 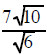 |
 multiply the
top and bottom by sqrt(6) multiply the
top and bottom by sqrt(6) |
the 10 and 6 are both factors under a radical sign so they can reduce each other |
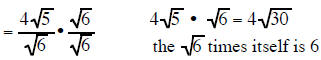 |
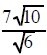 multiply the
top and bottom by sqrt(3) multiply the
top and bottom by sqrt(3) |
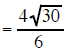 reduce4/6 reduce4/6 |
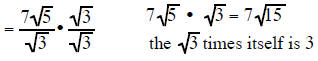 |
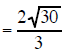 |
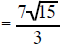 |
| Prev | Next |