Related Rates

Note: Formulas for volume, surface area, etc., are inside the front cover of your text.

Situation: Two or more quantities vary with time and are related by some equation. You
want to solve for a specified rate of change at a given instant.

Example: The radius of a circle is increasing at a constant rate of 2 cm/min. At what
rate is the area of the circle increasing when the radius is 10 cm?

Note: As the radius gets bigger, small changes in the radius yield big changes in area.
So, the area and the radius are increasing at different speeds and, as the radius gets
bigger, the area increases faster. You want to know how fast the area is growing at the
instant r = 10 cm. We indicate the rate of change of a quantity by its derivative with
respect to time t. That is, the rate of change of area A is 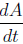; the rate of change of the
radius r is

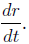
Recipe for Solving a Related Rates Problem

Step 1: Draw a good picture. Label all constant values and give variable names to any
changing quantities .
Step 2: Determine what information you know and what you want to find.
Step 3: Find an equation relating the relevant variables. This usually involves a for-
mula from geometry (inside the front cover of your text), similar triangles, the
Pythagorean Theorem, or a formula from trigonometry . Use your picture!
Step 4: Use implicit differentiation to differentiate the equation with respect to time t.
Step 5: Substitute in what you know from Step 2 and any information that your equa-
tion in Step 3 can give you and solve for the quantity you want. Do not substitute
before this step !

Related Rates Examples

1. Gas is escaping from a spherical balloon at a rate of 10 cubic feet per hour. At what
rate is the radius changing when the volume is 400 cubic feet ?

2. A man 7 feet tall is 20 feet from a 28-foot lamppost and is walking toward it at a
rate of 4 feet per second. How fast is his shadow shrinking at that moment? How
fast is the tip of the shadow moving?

3. A kite in the air at an altitude of 400 feet is being blown horizontally at the rate of
10 feet per second away from the person holding the kite string at ground level.
At what rate is the string being let out when 500 feet of string is already out?

4. One bicycle is 4 miles east of an intersection, travelling toward the intersection at
the rate of 9 miles per hour. At the same time, a second bike is 3 miles south of
the intersection and is travelling away from the intersection at a rate of 10 miles
per hour. At what rate is the distance between them changing? Is this distance
increasing or decreasing?

5. A 13-foot ladder is leaning against a wall and its base is slipping away from the
wall at a rate of 3 feet per second when it is 5 feet from the wall. How fast is the
top of the ladder dropping at that moment?

6. A point moves on the graph of y = x³ + x² + 1, the x-coordinate changing at a rate
of 2 units per second. How fast is the y- coordinate changing at the point (1, 3)?
How fast is the angle of inclination θ joining the point to the origin changing when
x = 1?