Systems of Linear Equations #2: Gaussian Elimination
Outline: Gaussian Elimination (Ax=b → Ux=c)
1) Review mechanics
2) Review modes of failures
3) The general pattern of GE
3) GE using Matrices (E and P)
4) General Rules of Matrix -Matrix Operations
Addition: (A+B)
Matrix Multiplication : AB
Matrix Powers : AP
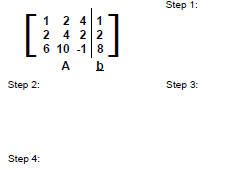
Gaussian Elimination on a 3x3 system of equations :
Example ( with row exchange):
x + 2y + 4z = 1
2x + 4y + 2z = 2
6x + 10y - z = 8
Matrix Vector form:
Augmented Matrix form:
Failure of Gaussian Elimination (review):
Example 2:
Example 1:
The overall Pattern of Gaussian Elimination:
A recursive Algorithm that reduces Ax=b to Ux=c
If successful: U will contain n pivots on the diagonal
( unique solution )
If Fails: U will contain at least 1 zero on the diagonal (no or ∞ solutions)
Gaussian Elimination using matrices:
Two Basic operations:
1) Elimination steps to zero out aij
2) Row exchanges to repair tempiojrary failure
BIG IDEA! We can design Matrices (E and P) to do this for
us
Elementary Elimination Matrices Eij :
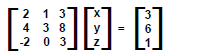
Matrix-Matrix Multiplication: C=AB
Column View:
Row View:
Other Examples: Diagonal Matrices
Left Multiplication: DA
Right Multiplication: AD
Does AD=DA (is matrix multiplication commutative ?)
Gaussian Elimination:
a sequence of Elementary Elimination Matrices
Point: Now we're doing real Linear Algebra !
( Algebra of matrices and vectors, not arithmetic )
Permutation Matrices
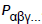
Again: AB≠BA in general
Gaussian Elimination:
a sequence of Elementary Elimination Matrices
Point: Matrices Do things!
An important Digression:
General rules of Matrix- Matrix Operations
Matrix Shape:
Matrix Matrix Addition : A+B
Properties of Matrix Addition: (follow from scalar and vector addition)
Matrix Matrix Multiplication: C=AB
Examples ( with numbers ):
Properties of Matrix Multiplication:
Theorem: Matrix Mult is associative.
If A,B,C are matrices of appropriate shapes, then A(BC)=(AB)C
Proof (sketch): Show A(Bc)=(AB)c
Another important Digression:
Operation costs of Matrix-vector and Matrix-Matrix multiplication
( order matters !)
An important Digression:
General rules of Matrix-Matrix Operations
Matrix Powers: AP
The matrix Inverse: A-1
Summary :
Gaussian Elimination using Matrices
| Prev | Next |