The Discriminant

The discriminant is a very useful concept when working with quadratic functions . It can tell you about the
number and types of solution you will have to a quadratic equation. Similarly, it can tell you about the
number of x - intercepts you will have on the graph of the quadratic equation. The discriminant is the part
of the quadratic formula that is underneath the radical, and thus is equal to b^2 - 4ac . Since quadratic
equations can have 0, 1, or 2 solutions, there are three different situations that can occur in quadratic
equations and the graphs of their related functions. Given the quadratic equation 0 = ax^2 + bx + c

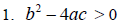
In this situation, since b^2 - 4ac is a positive number , our quadratic formula
will simplify to 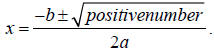And since the square root of
a positive number is another positive number,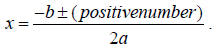

Here you will have two real solutions:

one being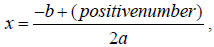

the other being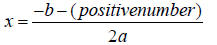

Similarly, since the quadratic equation 0 = ax² + bx + c is what you use to
find your x intercepts when you have the function f (x) = ax² + bx + c ,
you will also have two x -intercepts on the graph of your function.

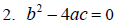
In this situation, since b^2 - 4ac is equal to zero, our quadratic formula will
simplify to 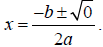And since the square root of zero is zero ,

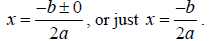This is just one real solution for x .
Similarly, since the quadratic equation 0 = ax² + bx + c is what you use to
find your x-intercepts when you have the function f (x) = ax² + bx + c ,
you will have only one x-intercept on the graph of the function.

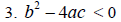
In this situation, since b^2 - 4ac is a negative number , our quadratic formula
will simplify to 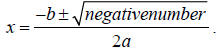But, we know that taking
the square root of a negative number yields an imaginary number (i), and
not a real number , we will get two imaginary solutions. We could also
state that we have zero real solutions to this equation. Again, similarly, since the
quadratic equation 0 = ax² + bx + c is what you use to find your x-intercepts
when you have the function f (x) = ax² + bx + c you will have no x-intercepts
on the graph of the function.