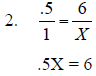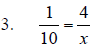Transformer Theory

Occupational Area: Electrical Technology
CTE Concept(s): Transformer windings, voltage, and current values
Math Concepts : Formula for calculating direct and inverse proportions, determining transformers ratios, determining unknown variables, and percent tolerance.
Lesson Objective:	Students will demonstrate knowledge of direct and inverse proportions and ratios as they apply to transformer theory and use these math concepts to meet industry specifications.
Supplies Needed:	1. A step down transformer 2. A calculator 3. A multi-meter 4. Textbook (Basic Mathematics for Electricity and Electronics) 5. Pencil, paper
THE "7 ELEMENTS"	TEACHER NOTES (and answer key)
1. Introduce the CTE lesson. Today we will discuss values of the primary and secondary side of a transformer and how to determine unknown quantities of turns, voltage, and current. Explain concepts of step up, step down, and equal transformers. Explain why it would be necessary to understand why there are different of winding turns, voltage, and current.	Speak to number of windings as proportional to value of voltage and as inversely proportional to values of current. Primary side is side that is supplied by voltage and secondary side taps to the load. Transformers are constructed to change values of voltage and current. We would need to lower voltage to operate signal systems (door chimes), communication systems, and computers.
2. Assess students’ math awareness as it relates to the CTE lesson. 1. Why calculate values of turns, voltage, and current? 2. Where would you use variable values and voltage and current in your home? 3. Where would you use a step up transformer versus a step down transformer? 4. Define the terms proportion , ratio, direct proportion, and inverse proportion. (Indirect proportion)	1. It’s necessary to match voltage and current to application and load. 2. Exps. Door chimes, communication devices, computers, low voltage lighting, fluorescent lighting, etc. 3. Fluorescent lighting and neon lighting. 4. Proportion – A value raising or lowering in value according to its supply. Ratio – A value compared to one . (2:1) Direct – values going in same direction as supply Inverse – values going is opposite direction of supply
3. Work through the math example embedded in the CTE lesson.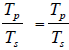 Given the above formula , what is the value of the secondary side voltage that has 1000 primary turns, 500 secondary turns, and a primary voltage of 1200 volts?	1. Set up formula. 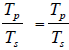2. Substitute values . 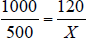3. Cross multiply 1000X = 500 * 120 1000X = 60,000 4. Isolate X X = 60,000/1000 5. Solve X – 60 volts 6. Ratio = 2:1
4. Work through related, contextual math-in-CTE examples. 1. Find the total primary voltage of a transformer that has 5000 turns on the primary, 1700 turns on the secondary, and 50 volts on the secondary. 2. Find the secondary current of a transformer that has 10,000 primary turns, 2,000 secondary turns, and 1 1amp of primary current? 3. Amperage is the unit of measurement for current and by the second problem we can see that current and voltage are inversely proportional. The terms inverse and indirect are often used interchangeably.
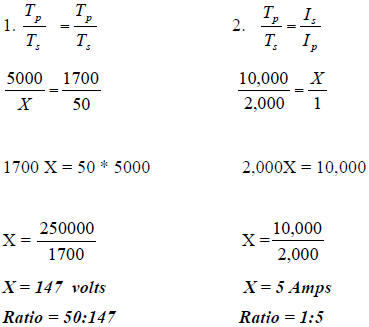5. Work through traditional math examples. 1. For every 10 degrees that the outside temperature rises, the temperature of a swimming pool rises 2 degrees. If the outside temperature rose 25 degrees, how many degrees warmer would the pool get? 2. If .5 inches of rain fell in one hour, how many hours will it take to get 6 inches of rain? 3. For every degree rise in temperature, a steam valve opens 10 percent. If the temperature rose 4 degrees, what percent of the valve opening increased?	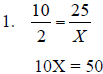X = 5 degrees Ratio = 5:1 X = 12 hours Ratio = .5:1 x = 40 percent opening Ratio = 1:4
6. Students demonstrate their understanding. 1. The students will work through a set of sample problems through guided application. The teacher will walk around the room and help those that need it and challenge those that understand it well. 2. The students will go to the white board and take turns doing practice problems. 3. The students will complete a homework assignment based on what was covered in transformer theory.	1. I will add more complicated problems as the students progress through the practice lesson. 2. At the white board, I will use an exemplary student to help demonstrate the concept of inverse proportion. 3. Homework assignment will come from text book.
7. Formal assessment. 1. Home work will be graded. 2. Students will receive a quiz on transformer proportions and ratios. 3. Students will be given math problems related to transformers that they are provided with. 4. The students will then energize the transformers and check values of primary and secondary voltages and currents. 5. A final test on transformer ratios and proportions will be given.	1. Homework from text. 2. Teacher made quiz. 3. Guide students in connecting transformer leads. 4.I will give the students transformers with values of: 120: 5. The test will include true/false, multiple choice , matching, open ended questions, and word problems.
Adaptations for special needs students.	Teacher Notes:
Instructional facilitator will spend extra time with special needs students on generic ratio and proportions mathematics.	Teacher will make up extra problems with simple values and progress to the more difficult.
Math Standards and Assessment Anchors addressed with this lesson.
M111.A.2.1. Solve problems using operations with rational numbers including rates and percents. M111.A.2.1. Solve problems using direct and inverse proportions