Calculus I - Math 124 Homework #7 Solutions
1. Water is being pumped at a rate of 4 ft3/second into a
trough that is 8 feet long with ends that have
the shape of an isosceles trapezoid with dimensions as shown in the figure.
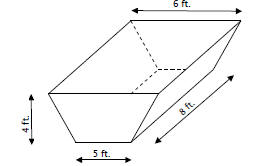
(a) How fast is the water level changing when the water
level has a height of 2 feet?
Quantities:
V = Volume of trough at time t
h = height of water at time t
Rates of Change: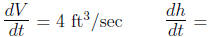 
? when h = 2
The area of a trapezoid is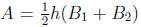 
if it has height h and bases
B1 and B2. Since the
trough is 8 feet long, the volume of the trapezoidal trough is
.
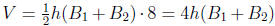Consider the figure below and the quantities listed in the figure.
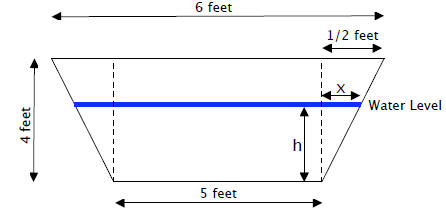
Given that B1 = 5 and B2 = 5 + 2x, we have that the volume
of the water in the trough is
V = 4h(5 + 5 + 2x) = 4h(10 + 2x)
The problem with this formula is that we are interested in the quantities V and
h and do not
have the rate of change of x. However, using similar triangles, we can write x
in terms of h .
 |
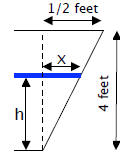We have  |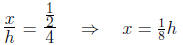
So, the volume of the trough is
.
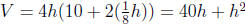Taking the derivative of each side with respect to t:
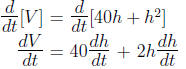
Solving for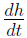 
when h = 2:
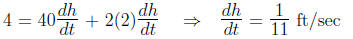
So, the water level is rising by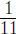 
ft/sec when
the water level is 2 feet.
(b) How long will it take to fill up the trough?
The trough has volume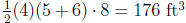 
. Since the water is
being pumped in at a rate of
4 ft3/sec, the trough will be filled after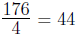
seconds.
2. Find the linearization of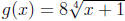 
at x = 15 and
use it to approximate g(15.05).
The linearization of g at x = 15 is given by L(x) = g'(15)(x − 15) + g(15).
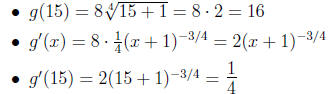
So, the linearization is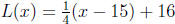 
.
Approximating g(15.05):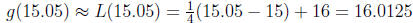 
3. Suppose we know that h(2) = −3 and h'(x) = x2 + 1.
(a) Use linear approximation to estimate h(1.9).
Linear Approximation: h(1.9) ≈ h'(2)(1.9 − 2) + h(2) = 5(1.9 − 2) − 3 = −3.5
(b) Is your estimate an over or underestimate? Explain.
(Hint: Consider the slope of h (x) near x = 2.)
Note that h'(x) < 5 for x < 2 and near 2. h'(x) > 5 for x > 2 and near 2. So,
the slope of h(x) is
positive and increasing near x = 2. (The tangent lines of h(x) are getting
steeper as x increases
with x near 2.)
So, the graph of h (x) near 2 and the tangent line at x = 2 look like the
following (not to scale).
 |
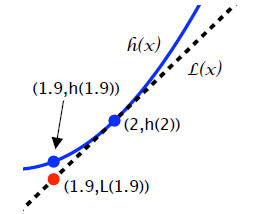Given how the slopes of h(x) are increasing, the tangent line will lie under the curve of h (x). So, the estimate from part (a) is an underestimate. |
4. Find the nth derivative of
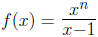for some positive integer n.
(Hint: If your first few derivatives are looking scary, take a look at the
original function and see if you can
approach it differently .)
Note: If you use the quotient rule or produce rule on
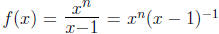, you will find that
your derivatives get messy rather quickly. Although, if you work to simplify
your answers after each
derivative using the quotient or product rule , you will find a nice pattern.
OR note that using long division , we have that
.
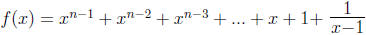The nth derivative of the first n terms of f is 0, i.e.,
.
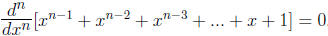So,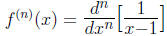 
.
It is easier to find a pattern for the derivatives of
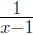. Doing so, you should find that
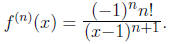
| Prev | Next |