Complex Numbers
Real Numbers
Let us think of the ordinary numbers as set out on a line which goes to infinity
in both positive
and negative directions . We could start by taking a stretch of the line near the
origin (that is, the
point representing the number zero) and putting in the integers as follows:
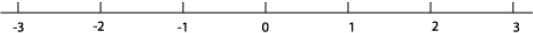
Next, we could add in rational numbers, such as ½ , 23/11,
etc., then the irrationals like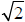 
,
then numbers like π, and so on, so any number you can think of has its place on
this line.
Now let’s take a slightly different point of view, and think of the numbers as
represented by a
vector from the origin to that number, so 1 is
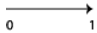
and, for example, –2 is represented by:
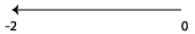
Note that if a number is multiplied by –1, the
corresponding vector is turned through 180
degrees. In pictures,
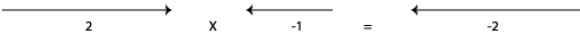
The “vector” 2 is turned through π, or 180 degrees, when
you multiply it by –1.
What are the square roots of 4?
Well, 2, obviously, but also –2, because multiplying the backwards pointing
vector –2 by –2 not
only doubles its length, but also turns it through 180 degrees, so it is now
pointing in the positive
direction. We seem to have invented a hard way of stating that multiplying two
negatives gives a
positive, but thinking in terms of turning vectors through 180 degrees will pay
off soon.
Solving Quadratic Equations
In solving the standard quadratic equation
ax2 + bx + c = 0
we find the solution to be :
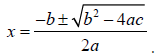
The problem with this is that sometimes the expression
inside the square root is negative. What
does that signify? For some problems in
physics, it means there is no solution. For example, if I
throw a ball directly
upwards at 10 meters per sec, and ask when will it reach a height of 20
meters,
taking g = 10 m per sec2, the solution of the quadratic equation for the time t
has a
negative number inside the square root, and that means that the ball
doesn’t get to 20 meters, so
the question didn’t really make sense.
We shall find, however, that there are other problems, in wide areas of physics,
where negative
numbers inside square roots have an important physical
significance. For that reason, we need to
come up with a scheme for interpreting
them.
The simplest quadratic equation that gives trouble is:
x2 + 1 = 0
the solutions being
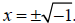
What does that mean? We’ve just seen that the square of a positive number is
positive, and the
square of a negative number is also positive, since
multiplying one negative number, which
points backwards, by another, which turns
any vector through 180 degrees, gives a positive
vector. Another way of saying
the same thing is to regard the minus sign itself , -, as an operator
which turns
the number it is applied to through 180 degrees. Now
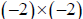has two such
rotations in it, giving the full 360 degrees back to the positive axis.
To make sense of the square root of a negative number, we need to find something
which when
multiplied by itself gives a negative number. Let’s concentrate for
the moment on the square root
of –1, from the quadratic equation above . Think of
–1 as the operator – acting on the vector 1, so
the – turns the vector through
180 degrees. We need to find the square root of this operator, the
operator
which applied twice gives the rotation through 180 degrees. Put like that, it is
pretty
obvious that the operator we want rotates the vector 1 through 90
degrees.
But if we take a positive number, such as 1, and rotate its vector through 90
degrees only, it isn’t
a number at all, at least in our original sense, since we
put all known numbers on one line, and
we’ve now rotated 1 away from that line.
The new number created in this way is called a pure
imaginary number, and is
denoted by i.
Once we’ve found the square root of –1, we can use it to
write the square root of any other
negative number—for example, 2i is the square
root of –4. Putting together a real number from
the original line with an
imaginary number (a multiple of i) gives a complex number . Evidently,
complex
numbers fill the entire two-dimensional plane. Taking ordinary Cartesian
coordinates ,
any point P in the plane can be written as (x, y) where the point
is reached from the origin by
going x units in the direction of the positive
real axis, then y units in the direction defined by i, in
other words, the y
axis.
Thus the point P with coordinates (x, y) can be identified with the complex
number z, where
z = x + iy.
The plane is often called the complex plane, and representing complex numbers in
this way is
sometimes referred to as an Argand Diagram.
Visualizing the complex numbers as two-dimensional vectors, it is clear how to
add two of them
together. If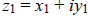 
, and
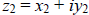, then 
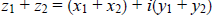. The real parts and
imaginary parts are added separately, just
like vector components.
Multiplying two complex numbers together does not have quite such a simple
interpretation. It
is, however, quite straightforward—ordinary algebraic rules
apply, with i2 replaced where it
appears by −1. So for example, to multiply
,
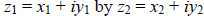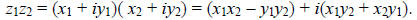
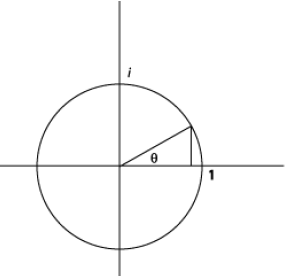
Polar Coordinates
Some properties of complex numbers are most easily understood if they are
represented by using
the polar coordinates (r , θ) instead of (x, y) to locate z
in the complex plane.
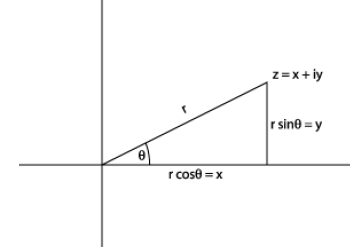
Note that z = x + iy can be written
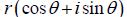from the
diagram above. In fact, this
representation leads to a clearer picture of
multiplication of two complex numbers:
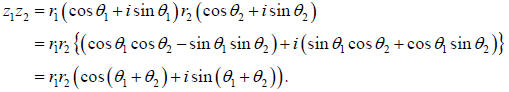
So, if
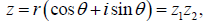
then
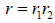
then
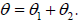
That is to say, to multiply together two complex numbers,
we multiply the r’s – called the moduli
– and add the phases, the θ ’s. The
modulus r is often denoted by | z |, and called mod z, the
phase θ is sometimes
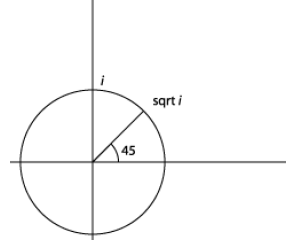
referred to as arg z. For example, |i| = 1, arg i = π/2.
We can now see that, although we had to introduce these complex numbers to have
a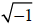 
, we
don’t need to bring in new types of numbers to get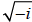
, or
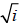. Clearly,
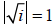, arg 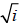= 45°.
It is on the circle of unit radius centered at the origin, at
45°, and squaring it just doubles the
angle
The Unit Circle
In fact this circle—called the unit circle—plays an important part in the theory
of complex
numbers. Every point on the circle has the form
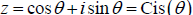,say
Since all points on the unit circle have |z| = 1, by
definition, multiplying any two of them
together just amounts to adding the angles, so our new function
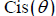satisfies
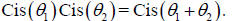
But that is just how multiplication works for exponents!
That is,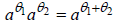 
for a any
constant, which strongly suggests that maybe our function
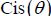is nothing but some constant a raised
to the power θ, that is,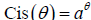
It turns out to be convenient to write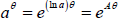 
say, where A = ln a.
This line of reasoning leads us to write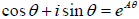 
Now, for the above “ addition formula ” to work for multiplication, A must be a
constant,
independent of θ. Therefore, we can find the value of A by choosing θ
for which things are
simple. We take θ to be very small—in this limit
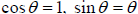, and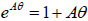 
dropping terms of order θ2 and higher.
Substituting these values into 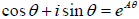gives A = i.
So we find:
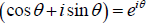
To test this result, we expand
:
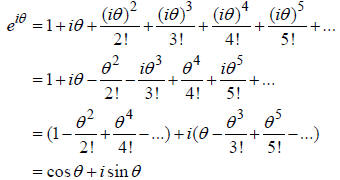
We write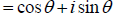 
in the last line because the series
in the brackets are precisely the
Taylor series for cosθ and sinθ confirming
our equation for 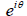. Changing the sign of θ it is
easy to see that
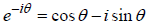
so
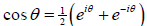,and
.
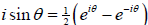Bottom Line: any complex number can be written:
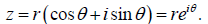
previous index next exercises
| Prev | Next |