Discrete Mathematics
Poker Problems
• What is a probability to contain one pair?
• What is a probability to contain two pairs ?
• What is a probability to contain a triple?
• What is a probability to contain royal flush?
• What is a probability to contain straight flush?
• What is a probability to contain straight?
• What is a probability to contain flush?
• What is a probability to contain full house?
• An r- combination with repetition allowed is
an unordered selection of elements where
some elements can be repeated
• The number of r -combinations with
repetition allowed from a set of n elements
is C(r + n –1, r)
• Soft drink example
Algebra of Combinations and
Pascal’s Triangle
• The number of r -combinations from a set
of n elements equals the number of (n – r)-
combinations from the same set.
• Pascal’s triangle: C(n + 1, r) = C(n, r – 1) +
C(n, r)
• C(n,r) = C(n,n-r)
• (a + b)n = ΣC(n, k)akbn-k
• Examples
• Show that ΣC(n, k) = 2n
• Show that Σ(-1)kC(n, k) = 0
• Express ΣkC(n, k)3k in the closed form
Probability Axioms
• P(Ac) = 1 – P(A)
• P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
– What if A and B mutually disjoint?
(Then P(A ∩ B) = 0)
Conditional Probability
• For events A and B in sample space S if
P(A) ≠ 0, then the probability of B given A
is:
P(A | B) = P(A ∩ B)/P(A)
• Example with Urn and Balls:
- An urn contains 5 blue and
Conditional Probability Example
• An urn contains 5 blue and 7 gray balls. 2
are chosen at random.
- What is the probability they are blue?
- Probability first is not blue but second is?
- Probability second ball is blue?
- Probability at least one ball is blue?
- Probability neither ball is blue?
• Imagine one urn contains 3 blue and 4
gray balls and a second urn contains 5
blue and 3 gray balls
• Choose an urn randomly and then choose
a ball.
• What is the probability that if the ball is
blue that it came from the first urn?
Bayes’ Theorem
• Extended version of last example.
• If S, our sample space, is the union of n
mutually disjoint events, B1, B2, …, Bn
and A is an even in S with P(A) ≠ 0 and k
is an integer between 1 and n, then:
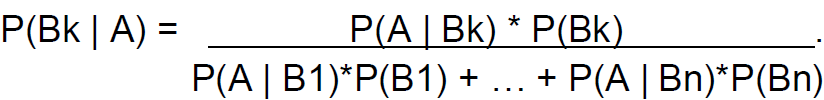
Application: Medical Tests ( false positives , etc.)
Independent Events
• If A and B are independent events,
P(A ∩ B) = P(A)*P(B)
• If C is also independent of A and B
P(A ∩ B ∩ C) = P(A)*P(B)*P(C)
• Difference from Conditional Probability can
be seen via Russian Roulette example.
Generic Functions
• A function f: X → Y is a relationship between
elements of X to elements of Y, when each
element from X is related to a unique element
from Y
• X is called domain of f, range of f is a subset of
Y so that for each element y of this subset there
exists an element x from X such that y = f(x)
• Sample functions:
– f : R → R, f(x) = x2
– f : Z → Z, f(x) = x + 1
– f : Q → Z, f(x) = 2
• Arrow diagrams for functions
• Non-functions
• Equality of functions:
– f(x) = |x| and g(x) = sqrt(x2)
• Identity function
• Logarithmic function
One-to-One Functions
• Function f : X → Y is called one-to-one
→ Y is called one-to-one
(injective) when for all elements x1 and x2
from X if f(x1) = f(x2), then x1 = x2
• Determine whether the following functions
are one-to-one:
– f : R → R, f(x) = 4x – 1
– g : Z → Z, g(n) = n2
• Hash functions
Onto Functions
• Function f : X → Y is called onto (surjective)
when given any element y from Y, there exists x
in X so that f(x) = y
• Determine whether the following functions are
onto:
– f : R →R, f(x) = 4x – 1
– f : Z →Z, g(n) = 4n – 1
• Bijection is one-to-one and onto
• Reversing strings function is bijective
Inverse Functions
• If f : X → Y is a bijective function, then it is
possible to define an inverse function f-1: Y
→ X so that f-1(y) = x whenever f(x) = y
• Find an inverse for the following functions:
– String-reverse function
– f : R → R, f(x) = 4x – 1
• Inverse function of a bijective function is a
bijective function itself
Pigeonhole Principle
• If n pigeons fly into m pigeonholes and n > m,
then at least one hole must contain two or more
pigeons
• A function from one finite set to a smaller finite set
cannot be one-to-one
• In a group of 13 people must there be at least two
who have birthday in the same month?
• A drawer contains 10 black and 10 white socks.
How many socks need to be picked to ensure that
a pair is found?
• Let A = {1, 2, 3, 4, 5, 6, 7, 8}. If 5 integers are
selected must at least one pair have sum of 9?
• Generalized Pigeonhole Principle: For any function f : X
→ Y acting on finite sets, if n(X) > k * N(Y), then there
exists some y from Y so that there are at least k + 1
distinct x’s so that f(x) = y
• “If n pigeons fly into m pigeonholes, and, for some
positive k , m >k*m, then at least one pigeonhole
contains k+1 or more pigeons”
• In a group of 85 people at least 4 must have the same
last initial.
• There are 42 students who are to share 12 computers.
Each student uses exactly 1 computer and no computer
is used by more than 6 students. Show that at least 5
computers are used by 3 or more students.
Composition of Functions
• Let f : X → Y and g : Y → Z, let range of f be a
subset of the domain of g. The we can define a
composition of g o f : X →Z
• Let f,g : Z → Z, f(n) = n + 1, g(n) = n2. Find f o g
and g o f. Are they equal?
• Composition with identity function
• Composition with an inverse function
• Composition of two one-to-one functions is oneto-
one
• Composition of two onto functions is onto
Cardinality
• Cardinality refers to the size of the set
• Finite and infinite sets
• Two sets have the same cardinality when there is
bijective function associating them
• Cardinality is is reflexive, symmetric and transitive
• Countable sets: set of all integers, set of even numbers,
positive rationals (Cantor diagonalization)
• Set of real numbers between 0 and 1 has same
cardinality as set of all reals
• Computability of functions
| Prev | Next |