Elementary Number Theory and Methods of Proof
Proof and Counterexample
• Discovery and proof
• Even and odd numbers
– number n from Z is called even if
∃k
∈ Z, n = 2k
– number n from Z is called odd if
∃k
∈ Z, n = 2k + 1
• Prime and composite numbers
– number n from Z is called prime if
∀r, s ∈ Z, n = r * s
→ r = 1 ν s = 1
– number n from Z is called composite if
∃ r, s ∈ Z, n = r * s
Λ r > 1 Λ s > 1
Proving Statements
• Constructive proofs for existential statements
• Example: Show that there is a prime number that
can be written as a sum of two perfect squares
• Universal statements: method of exhaustion and
generalized proof
• Direct Proof:
– Express the statement in the form:
∀x ∈ D, P(x)
→
Q(x)
– Take an arbitrary x from D so that P(x) is true
– Show that Q(x) is true based on previous axioms ,
theorems, P(x) and rules of valid reasoning
Proof
• Show that if the sum of any two integers is
even, then so is their difference
• Common mistakes in a proof
– Arguing from example
– Using the same symbol for different variables
– Jumping to a conclusion
– Begging the question
Counterexample
• To show that the statement in the form “∀X ∈ D,
P(x) → Q(x)” is not true one needs to show that
the negation, which has a form “∃X ∈ D, P(x)
Λ
~Q(x)” is true. x is called a counterexample.
• Famous conjectures:
– Fermat big theorem: there are no non- zero integers x, y,
z such that xn + yn = zn, for n > 2
– Goldbach conjecture: any even integer can be
represented as a sum of two prime numbers
– Euler’s conjecture: no three perfect fourth powers add
up to another perfect fourth power
Exercises
• Any product of four consecutive integers is
one less than a perfect square
• To check that an integer is a prime it is
sufficient to check that n is not divisible by
any prime less than or equal to Ön
• If p is a prime, is 2p – 1 a prime too?
• Does 15x3 + 7x2 – 8x – 27 have an integer
zero?
• Real number r is called rational if
∃p,q ∈ Z, r = p / q
• All real numbers which are not rational are
called irrational
• Is 0.121212… a rational number
• Every integer is a rational number
• Sum of any two rational numbers is a
rational number
Divisibility
• Integer n is a divisible by an integer d, when
∃k ∈ Z, n = d * k
• Notation: d | n
• Synonymous statements:
– n is a multiple of d
– d is a factor of n
– d is a divisor of n
– d divides n
• Divisibility is transitive: for all integers a, b, c, if a
divides b and b divides c, then a divides c
• Any integer greater than 1 is divisible by a prime
number
• If a | b and b | a, does it mean a = b?
• Any integer can be uniquely represented in the
standard factored form:
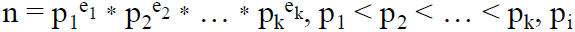 is a
is a
prime number
Exercises
• Prove or provide counterexample:
– For integers a, b, c: (a | b) → (a | bc)
– For integers a, b, c: (a | (b + c)) → (a | b Λ a | c)
• If 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * m = 151 * 150 *
149 * 148 * 147 * 146 * 145 * 144 * 143, does
151 | m?
• Show that an integer is divisible by 9 iff the sum
of its digits is divisible by 9. Prove the same for
divisibility by 3.
• Show that an integer is divisible by 11 iff the
alternate sum of its digits is divisible by 11
Quotient and Remainder
• Given any integer n and positive integer d, there
exist unique integers q and r, such that n = d * q +
r and 0 ≤ r < d
• Operations: div – quotient, mod – remainder
• Parity of an integer refers to the property of an
integer to be even or odd
• Any two consecutive integers have opposite parity
• The square of an odd integer has reminder 1 when
divided by 8 (read in book)
Exercises
• Show that a product of any four consecutive
integers is divisible by 8
• Show that the sum of any four consecutive
integers is never divisible by 4
• Show that any prime number greater than 3
has remainder 1 or 5 when divided by 6
| Prev | Next |