Fractions of Whole Numbers
Equivalent or Equal Fractions
Equivalent fractions are fractions that have the same value or represent
the same part of an object. If a pie is cut into two pieces, each piece is also
one-half of the pie. If a pie is cut into 4 pieces, then two pieces represent
the
same amount of pie that 1/2 did. We say that 1/2 is equivalent or equal
to 2/4 and we write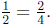 
The Fundamental Law of Fractions describes the general relationship be-
tween equivalent fractions.
The Fundamental Law of Fractions
For any fraction a/b and any nonzero whole number c we have
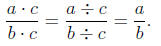
Example 18.2
Show that the fraction 6/14 is equivalent to 9/21 .
Solution .
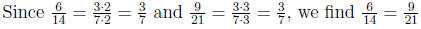
The following theorem shows that two fractions are
equivalent if and only if
their cross- products are equal .
Theorem 18.1
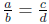if and only if ad = bc.
Proof.
Suppose first that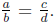 
Since
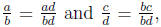we must have
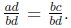
But this is true only when ad = bc.
Conversely, if ad = bc then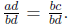 
By the
Fundamental Law of Fractions
we have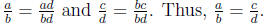 
Example 18.3
Find a value for x so that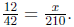 
Solution.
By the above theorem we must have 42*x = 210*12.
But 210*12 = 60*42
so that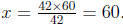 
Simplifying Fractions
When a fraction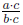 
is replaced with
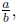we say that
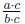has been simplified.
We say that a fraction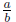 
is in simplest form
(or lowest terms ) if a and b
have no common divisor greater than 1. For example, the fraction
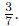
We write a fraction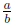 
in simplest form by
dividing both a and b by the
GCF (a,b).
Example 18.4
Find the simplest form of each of the following fractions.
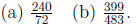
Solution.
(a) First, we find GCF(240,72). Since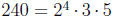 
and
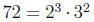we nd
GCF(240, 72) =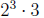 
= 24.
Thus,
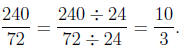
(b) Since 399 =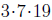 
and
483 =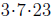 
we have GCF(399, 483) = 3*7 = 21.
Thus,
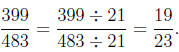
Example 18.5
Simplify the fraction 54/72 .
Solution.
Since GCF(54, 72) = 18 then
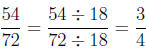
Practice Problems
Problem 18.8
Show that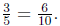 
Problem 18.9
Use drawings of fractions strips to show that 3/4 , 6/8 , and 9/12 are
equivalent.
Problem 18.10
Write each fraction in simplest form.
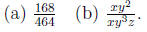
Problem 18.11
Two companies conduct surveys asking people if they favor stronger controls
on air pollution. The first company asks 1,500 people, and the second asks
2,000 people. In the first group, 1,200 say yes. Make up results for the second
group that would be considered equivalent.
Problem 18.12
Find four different fractions equivalent to 4/9 .
Problem 18.13
Fill in the missing number to make the fractions equivalent.
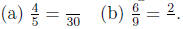
Problem 18.14
Rewrite the following fractions in simplest form.
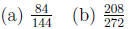
Problem 18.15
Find the prime factorizations of the numerators and denominators of these
fractions and use them to express the fractions in simplest form.
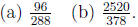
Problem 18.16
If a fraction is equal to 3/4 and the sum of the numerator and denominator is
84, what is the fraction?
Problem 18.17
Determine if each of the following is correct.
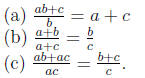
Problem 18.18
If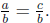 
what must be true?
Problem 18.19
Solve for x .
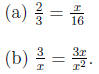
Problem 18.20
Rewrite as a mixed number in simplest form.
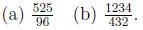
Problem 18.21
I am a proper fraction. The sum of my numerator and denominator is one-
digit square . Their product is a cube. What fraction am I?
Comparing and Ordering Fractions
If we place the fractions 2/7 and 5/7 on the fraction number line we notice
that 2/7 is to the left of 5/7. This suggests the following definition.
We say that a/b is less than c/b , and we write
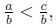if and only if a < c.
The above definition compares fractions with the same denominator. What
about fractions with unlike denominators? To compare fractions with unlike
denominators, say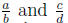 
with
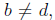we compare the fractions
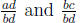
since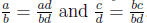 
By the above definition, it follows
that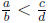 
if and
only if ad < bc.
This establishes a proof of the following theorem.
Theorem 18.2
If a, b, c, d are whole numbers with b ≠ 0, d ≠ 0 then
if and only if
ad < bc.
Example 18.6
Compare the fractions 7/8 and 9/11 .
Solution.
Since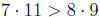 
we have
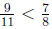
We conclude this section with the following question.
Given two fractions
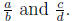Is there a fraction between these two
fractions?
The answer is a rmative according to the following theorem.
Theorem 18.3 (Density Property)
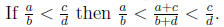
Proof.
Since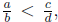 
by Theorem 18.2 we have ad < bc.
Add cd to both sides to
obtain ad + cd < bc + cd.
That is, (a + c)d < (b + d)c or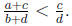 
Similarly, if we add ab to both sides of ad < bc we find ad + ab < bc + ab or
a(b + d) < b(a + c).
Thus,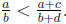
Example 18.7
Find a fraction between the fractions 9/13 and 12/17 .
Solution.
Since 9*17 < 12*13 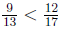we have 
By the previous
theorem we have
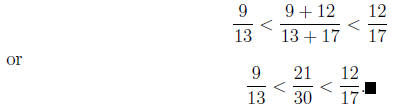
Practice Problems
Problem 18.22
Show that
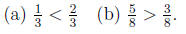
Problem 18.23
Compare the pairs of fractions.
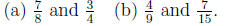
Problem 18.24
You have two different recipes for making orange juice from concentrate. The
first says to mix 2 cups of concentrate with 6 cups of water. The second says
to mix 3 cups of concentrate with 8 cups of water. Which recipe will have a
stronger orange flavor?
Problem 18.25
A third grader says that 1/4 is less than 1/5 because 4 is less than 5. What
would
you tell the child?
Problem 18.26
Find a fraction between 3/4 and 7/8 .
Problem 18.27
Order the following fractions from least to greatest .
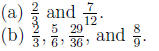
Problem 18.28
Compare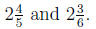 
Problem 18.29
If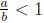 
, compare the fractions
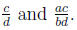
Problem 18.30
Find a fraction between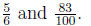 
| Prev | Next |