General Composition of Functions

The Composition of Two Functions

In the last lecture, we discussed the stretching and shifting of functions. Stretching and shifting are just two
examples of a general phenomenon called the composition of functions. The composition of two functions is
the topic for today’s lecture.

Let f(x) and g(x) be two real valued functions whose domains are the real numbers. Polynomial functions
and sine and cosine functions are examples of functions which fit this description. Suppose that we took a
number x and applied the function f to it. We would get as our output the number f(x). Suppose now that
we applied the function g to the number f(x). We would get another number as our output g(f(x)).

The key point for this section is that we can think of the action of starting with x, then applying f, then
applying g, not just as two functions being applied one after another, but as one function, a composition of
f and g. Our new function, which we write as 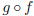and speak as “g compose f” or, perhaps more precisely,
as “g after f,” takes every real number x and gives us back the number g(f(x)).

You can think about the composition of functions in the following way: before, we described a function
as a machine, which takes in raw material, its domain, and gives out a finished product, its range. Suppose
that we have two such machines, one called f, the other called g. Suppose further that the raw material for
g is the finished product of f . Then we could imagine setting up these two machines in an assembly line ,
so that as soon as the finished product comes out of the machine f, it goes into the machine g. How do we
envision the composition 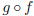? What we do is imagine placing a big box around both the machine f and
the machine g, so that when raw material goes into the machine f, we do not see it again until it comes
out of the machine g. Now, if after we put this big box around f and g, someone looked at this big box
and saw raw material going in and finished product coming out, he would assume that this big box was a
single machine, even though we know that in reality it is two machines, working one after the other. That
person would be perfectly correct , however, to assume that he is seeing only one machine, because it does
not matter how the machine works inside: all that matters is that it has an input and an output. Now we,
knowing that this big box encompasses two machines, want to label the box so as to inform people that this
box contains the machine g working directly after the machine f. We do this by labelling the big box as
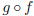. It is still a single machine, but now people know how it works inside.

Let us do a few examples of composition using formulas instead of big boxes. Let f(x) = cos x and let
g(x) = x^3. We get the formula for the composition 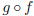by substituting the formula for f(x) in for x in the
formula for g(x). In the case, we substitute cos x for x in g(x) = x^3, so that we get

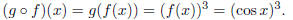
Now let us try the composition the function we get by first applying g and then applying f. This time,
we substitute x^3 in for x in f(x) = cos x. The result is

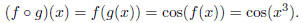
This example illustrates a very important point about composition: usually, the function does not
equal the function 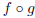. The order in which you compose two functions matters a great deal. For another
example, take f(x) = 2x and g(x) = x^2. Then

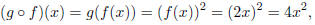
and

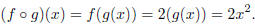
If you were to plot these two compositions alongside the graph of x^2, you would see that the first, 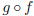, is
a horizontal stretch of the graph of x ^2, while the second, 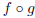, is a vertical stretch of that parabola . This
leads us into the next section.

Stretches and Shifts as Compositions

For more examples of composition, we study stretches and shifts of functions again. Remember that we
stated that g(x) is a vertical stretch of f(x) if g(x) = af(x). Let h(x) = ax. Another way to write the
definition of a vertical stretch is to write g(x) as a composition of f(x) and h(x). Specifically, g(x) is a
vertical shift of f(x) if g(x) = (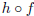)(x) for some real number a. We see that this is true by finding the
formula for :

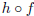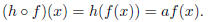
We defined g(x) to be a horizontal stretch of f(x) if g(x) = f(ax) for some real number a. If we define
h(x) = ax again, then we quickly see that a horizontal stretch can also be understood to be a composition
of two functions, specifically, g(x) = (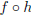)(x), since when we work out the formula for 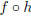, we get

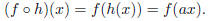
So, for a vertical stretch, we apply h to the range of f, and for a horizontal stretch, we apply h to the
domain of f. This should make intuitive sense to you: The range of f corresponds to the vertical axis on the
xy-plane, and the domain of f corresponds to the horizontal axis. Thus, if you want to change the graph of
f(x) horizontally, you want to act on its domain, and it you want to change its graph vertically, you act on
its range.

We said that a function g(x) is a vertical shift of f(x) if for some real number b we have that g(x) =
f(x)+b. How could we write g(x) as the composition of two functions? One way to do it is to let k(x) = x+b.
Then

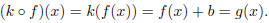
So g is the composition of k after f.
We defined g(x) to be a horizontal shift of f(x) if g(x) = f(x + b) for some real number b. Clearly g(x)
is the composition of two functions in this case as well: setting k(x) = x + b again, we see that

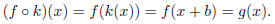
Notice how for horizontal shifts k acts on the domain of f, and for vertical shifts, k acts on the range, just
as in the case of stretches.

Seeing Functions as Compositions

In the previous section , we took known functions, the stretches and shifts of f(x), and rewriting them as
the composition of two functions. This is the most important skill that you must learn about compositions:
recognizing that a function is the composition of two other functions. There are no simple rules for breaking
up a function into the composition of two other functions; the best way to learn how this skill is to see a lot
of examples.

First, let us take the example h(x) = sin²x+9 sin x+8. We see that this is a trigonometric polynomial,
that is, a polynomial of sin x instead of x. This should suggest to you how to write this function as the
composition of two other functions: the inside function, the one we do first, should be sin x, and the outside
function should be a polynomial. Specifically, take f(x) = sin x and g(x) = x² + 9x + 8. Then

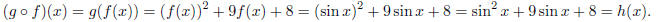
For the next example, let h(x) = (2x² + 3x - 7)⁴. This function is a polynomial raised to the fourth
power. It stands to reason that, to write this function as the composition of two other functions, g(x) after
f(x), the inside function, f(x), should be the polynomial being raised to the fourth power , and the outside
function, g(x), should be x⁴. So let f(x) = 2x² + 3x - 7 and let g(x) = x⁴. Then

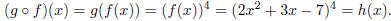
So h(x) is the composition of g(x) after f(x).
Notice the general principle at work here: we look for an inside function, a function being acted upon,
and we let this function be f(x). We then figure out how f(x) is being acted upon, and we label the function
that is doing the action by g(x). Let us try two more examples.

Let h(x) = cos(x¹⁷). We can see that cos x is acting on x¹⁷. So we let f(x), the inside function, be equal
to x¹⁷, and we let g(x), the outside function, be equal to cos x. Then we get that

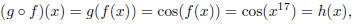
so our choices of g(x) and f(x) work.
Finally, take h(x) = sin(cos(x²)). This example presents us with a choice. First, we could take the inside
function to be f(x) = cos(x²) and the outside function to be g(x) = sin x. Then

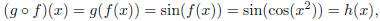
so this choice of f(x) and g(x) work. We could also have chosen the inside function to be x² and the outside
function to be sin(cos x). So let m(x) = x² and n(x) = sin(cos x). Then we get that

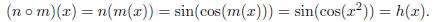
So now we have two equally valid ways to break up h(x) into the composition of two functions. You may
also notice that we could see h(x) as the action of three different functions , one after the other after the
other. In this case, take p(x) = x², q(x) = cos x, and r(x) = sin x. Then we define the function 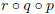to
be a function we get by first acting on x by p, then acting on p(x) by q, and then acting on q(p(x)) by r.
This triple composition is equal to h(x):

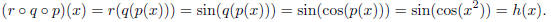
So now we have three different ways to break up h(x) into the composition of two or more functions. We
will use this skill in the next lecture when we discuss how to differentiate the composition of functions using
the chain rule.