Linear Equations Worksheet-Solutions
1. Given is the line with equation y = 3x − 2.
(a) Find five points on the line and arrange them in a table.
Answer
| y = 3x − 2 | |
| x | y |
| -2 | -8 |
| 0 | -2 |
| 1 | 1 |
| 3 | 7 |
| 10 | 28 |
(b) Graph the line .
Answer See the graph on the last page.
(c) Find the x- intercept and the y -intercept.
Answer To find the x-intercept let y = 0 in y = 3x
− 2 and solve for x.
Thus, the x- intercept is the point ( 2/3 , 0).
To find the y-intercept let x = 0 in y = 3x − 2 and solve for y .
Thus, the y-intercept is the point (0,−2).
2. Find the slope-intercept form of the equation of the
line through the points (2, 7)
and (5, 2) and graph it .
Answer First calculate the slope.
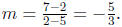 So far we have
So far we have
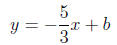
To solve for b we substitute the coordinates of a point on
the line, for example (2, 7).
Then at the point (2, 7) we have
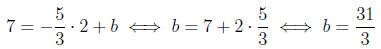
and so the answer is
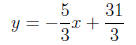
We should check our work by verifying that the other point
also lies on the line.
In other words, substituting the point (5, 2) we should obtain an identity.
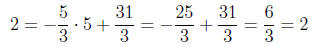
3. Consider the line passing through the point (2, 3) with slope m = −1.
(a) Write down the point-slope equation of the line.
Answer
y − 3 = −(x − 2)
(b) Write the equation in the slope-intercept form.
Answer
y = −x + 5
(c) Find all intercepts.
Answer The x-intercept is the point (5, 0) and the y-intercept is the point (0, 5).
4. Consider the line y = 2x + 3.
(a) Find the equation in slope-intercept form of a parallel line through (2, 5).
Answer The given line has slope m = 2 so we are
looking for a line of the
form y = 2x + b and containing the point (2, 5). Substituting x = 2 it follows
that b = 1 in order for y = 5. Thus, we obtain
y = 2x + 1
(b) Find the equation of a perpendicular line through (2, 7).
Answer The line has slope m = 2 so
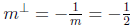 and a perpendicular line
and a perpendicular line
will have the form
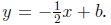 Substituting the point (2, 7) and solving for b
Substituting the point (2, 7) and solving for b
we obtain
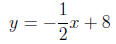
5. Consider the line L given by 2x + 3y = 6.
(a) Find the slope and intercepts of the line.
Answer In the slope-intercept form we have
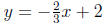 so the slope is
so the slope is
m = −2/3 . The x-intercept is the point (3, 0) and the y-intercept is the point
(0, 2).
(b) Find a point on the line and a point not on the line.
Answer (0, 0) does not lie on the line, but (3, 0) does.
(c) Write the equation of the line in point-slope form.
Answer The slope we already know to be m = −2/3 and
we can choose the
point (3, 0), so
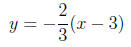
(d) Find the equation of a line perpendicular to L, but
passing through the same
x-intercept as the line L.
Answer We have m = −2/3 so
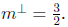 In slope-intercept form we have
In slope-intercept form we have
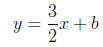
and we need to have this line pass through the point (3,
0). Substituting we
find that b = −9/2 and so the answer is
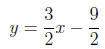
6. Solve:
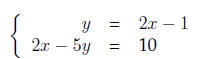
Answer Proceed by elimination: rewrite the system
of equations and add them.
We have
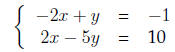
and whence −4y = 9
 y = −9/4 . Then we substitute y = −9/4 into the first equation
y = −9/4 . Then we substitute y = −9/4 into the first equation
and solve for x and obtain x = −5/8 . To make sure that
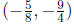 is the solution we
is the solution we
check that it also solves the second equation:
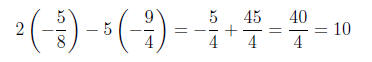
7. Derive the point-slope form of the equation for a line by following these steps .
(a) Let L be the line passing through the fixed point
(x1, y1) and an arbitrary point
(x, y).
(b) Find the general formula for the slope of L.
Answer The slope of L is given by
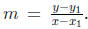 Multiplying thru by (x − x1) we
Multiplying thru by (x − x1) we
obtain the point-slope form.
8. *Write down a system of 3 linear equations that has
(a) exactly one solution
Answer All the above problems have exactly one solution. Take for example
problem 6 and introduce a third line which passes through the solution
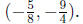 We use the slope-intercept form with an arbitrary slope, say m = 2.
We use the slope-intercept form with an arbitrary slope, say m = 2.
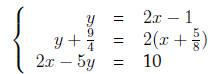
(b) no solution
Answer The only three lines in the plane that do not intersect are parallel
lines. We can take for example the line 2x − 5y = 10 and pick 3 different
y -intercepts.
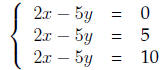
(c) infinitely many solutions
Answer Infinitely many solutions occur when the three lines are in fact the
same line. That is, we have three parallel lines with the same y-intercept.
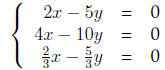
| Prev | Next |