Linear Systems of Equations
Outline
Preliminaries
Introductions.
Sign -up list.
Syllabus.
Homework 1.
Course Overview.
Linear Systems of Equations .
Key Points on Syllabus
Quizzes every Tuesday.
Homeworks due begining of class.
NO LATE HOMEWORKS.
Late projects are accepted with 20% penalty.
NO MAKEUP EXAMS. If you miss an exam, or if
you do
badly, the weight of that exam will be added
to the final .
Homework 1
Due Tuesday, Aug. 30, at beginning of class.
Section 1.1: 4,6,8,10,12,14,16,18,20, 23,
24, 30, 33,34
Section 1.2: 2,4,8,10,12, 15, 18, 20, 21,22,
24, 26, 29,
31, 33
Course Overview
Dealing with many
variables and many equations.
Linearity.
Abstraction and Proofs.
A linear equation in the variables
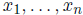is an equation
that can be written in the form
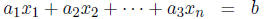
Examples:
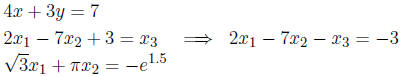
Not Linear:
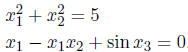
Systems of Linear Equations
An m × n system of linear equations has the form:
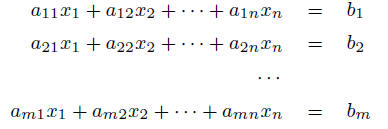
Note: each equation involves the same variables,
.
A solution of the
system is a list of numbers (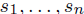
) that makes
each equation
true when the values 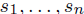are substituted for
, respectively.
Example: The system
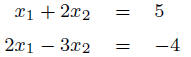
has solution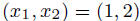 
.
A Geometric View
Exercises:
Graph the solution
set of the equation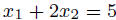 
. (Question: why does it
make
sense to call this a linear equation?).
Graph the line
defined by the equation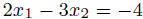 
.
Where do these two
lines intersect?
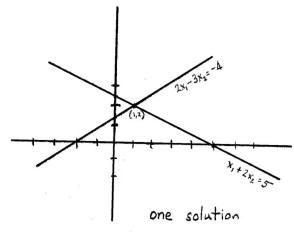
Geometry 2
But this doesn’t always work:
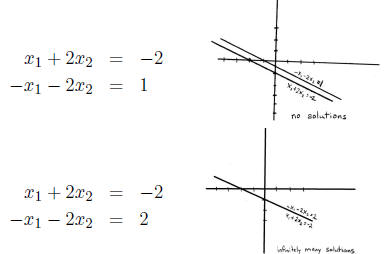
Solutions of Linear Systems
A system of linear equations has either
1. No solution (inconsistent).
2. Exactly one solution. (consistent).
3. Infinitely many solutions. (also consistent).
Matrix Notation
Since all the equations in a linear system involve the
same variables, we can economize by
writing only the coefficients (not the variables) in a compact form called the
Augmented
matrix:
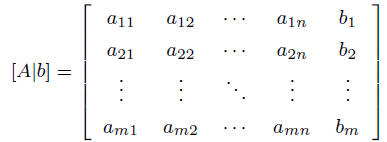
Example:
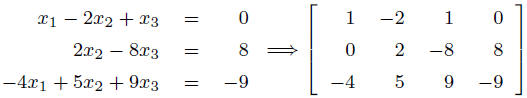
Solving Linear Systems
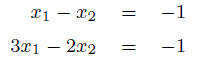
Add (-3) times equation 1 to equation
2.
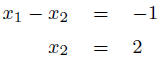
Add equation 2 to equation 1.
 |
 |
|
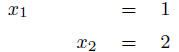
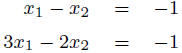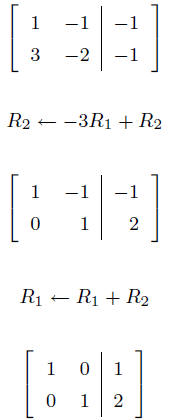Add (-3) times equation 1 to equation 2. |
|
 |
|
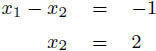| Add equation 2 to equation 1. | |
 |
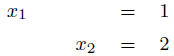Elementary Row Operations
1. (Replacement) Add c times row j to row i (replacing row
i, and leaving row j unchanged).
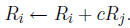
2. (Interchange) Interchange row i and row j.
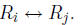
3. (Scaling) Multiply row i by a constant c ≠ 0.
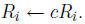
KEY FACT: Elementary row operations do not alter the
solution set.
Gauss- Jordan Elimination
Apply a sequence of elementary row operations to get the matrix into a form that
is
trivial to solve.
Example: A series of
elementary row operations yields the following transformation
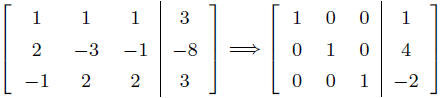
The righthand matrix corresponds to the system of equations:
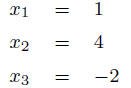
Trivial to solve!!
The above matrix is
in a special form called the reduced row echelon form.
| Prev | Next |