Math 320 Group Exam

Group Exam

1. For n a natural number, let f (n) represent the number of factors of n . For example,
f (6) = 4, because 6 has four factors : 1, 2, 3, and 6.

a. Make a table of n and f (n) for n =1 to n =25. Describe any patterns you
notice in your table

b. Let p be a prime. Find f ( p) and prove your result.

c. Find f ( p² ) and f ( p³ ) and prove your results.

d. Find f ( pⁿ ) and prove your result.

e. Now let p,q and r be primes. Find f ( pq) , f ( p²q) and f ( pqr) and prove
your results.

f. How can you find f (n) , for any n ?

2. For n a natural number, let g(n) represent the number of natural numbers less than n
and relatively prime to it. For example, g(5) = 4, because 1,2, 3, and 4 are less than 5
and the greatest common factor of 5 and each of these numbers is 1. Also, g(12) = 4,
because 1, 5, 7, and 11 are the only four natural numbers less than 12 that are relatively
prime to 12.

a. Make a table of n and g(n) for n=1 to n=25. Describe any patterns you
notice in your table.

b. Let p be a prime. Find g( p) and prove your result.

c. Find g( p² ) and g( p³ ) and prove your results.

d. Find g( pⁿ ) and prove your result.

e. From your table and your results above, can you find a method for
determining g(n) for any n ?

f. Below is an example that we will use to illustrate an amazing property of
g (n) . We illustrate for n =12. Start by writing all fractions with denominator
n and numerators from 0 to n -1:

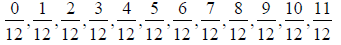
Now simplify and group by denominators (simplify 0/n to 0/1 ):

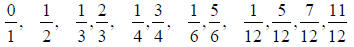
For any n, how many groups will there be (i.e. how many different
denominators)?

Given the denominator of a group , within the group, how many different
numerators will there be?

Use the above to illustrate an amazing property of g(n) .

3. In this problem, we will explore powers in various modulos.

a. Either using Excel (or by hand), for each n from 3 to 12, make a table of the
first 2 n powers of 2, 3, …, n -1, mod n . For example, here is a table mod 7:

Note that it is better to reduce by the modulo , as you go along to avoid
round off errors. For example, to compute 4⁴, you can multiply 4³ ≡1 (mod 7) by 4 to get
4, instead of computing 4⁴=256, and then finding that 256 ≡ 4 (mod 7).

b. Look for patterns in your tables. Try to justify as many as you can.

c. The order of a mod n , is defined as the smallest k such that a^k ≡1(mod n).
For example, using the table above, we can see that the order of 6 mod 7 is 2,
the orders of 2 and 4 mod 7 are 3, and the orders of 3 and 5 mod 7 are 6.

The order of a mod n is undefined if no power of a is ever equal to 1 mod
n . Determine when the order of a is defined and when it is undefined. For
which mods are the orders of 2, 3, …, n-1 always defined?

d. For this part of the problem, only use mods, n , for which the orders of 2, 3,
…, n -1 are always defined. What are the possible orders in each of these
mods? How many numbers have each order? Prove as much as you can, and
also relate to the first few problems.

e. Now explore the a ’s that do have a defined order, in the mods where some
a ’s don’t have a defined order (for example, in mod 4, the order of 3 is 2, but
the order of 2 is undefined). How many such a ’s are there? What orders do
they have?

f. In the chart in part a, the 6^thand 12^thpowers mod 7 are 1 for all a ’s. Explore
similar patterns other modulos. Here is an example that might help you prove
a result here:

Note that mod 7, we have: 3*1=3, 3*2=6, 3*3=2, 3*4=5, 3*5=1, and
3*6=4. Now if we multiply all of the above together, we get
3*1*3*2* 3*3* 3*4* 3*5* 3*6. Rearranging, we get 3⁶*(1*2*3*4*5*6). Now we also
know that this product is equal to 1*2*3*4*5*6. Fill in the details…and make more
general.

4. In this problem, we relate the results of the first few problems to patterns in decimals
and expansions in various bases.

a. Read the attached handout about why the standard long division algorithm
works. Use the standard long division algorithm to show that 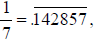and explain
why the algorithm works.

b. Note that 10 ≡ 3(mod 7),10² = 2(mod 7),10³ ≡ 6(mod 7) , 10⁴ ≡ 4(mod 7),
10⁵ ≡ 5(mod 7) , and 10⁶ ≡1(mod 7) . Show where the set of remainders, {3, 2, 6, 4, 5, 1}
appear in the division algorithm for computing the expansion of 1/7 in part a. Adapt this
connection to show how to compute the period of 1/13 without actually finding the
decimal expansion of 1/13 .

c. Explain how to find the period of 1/p for any prime p in any base b , without
actually computing the expansion of 1/p. Make up a few examples to illustrate your
method.

d. What connections do you see between your results in the first three problems
and patterns you observed in looking at the expansions of unit fractions in various bases?

e. The expansions of 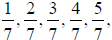and 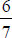are all strictly repeating, with shifted
versions of the same six digits. The computations below give insight into this pattern:

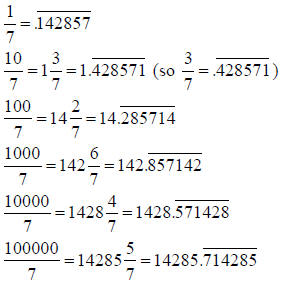
Note that the numerators of the fractions appear in the same order {3, 2, 6, 4, 5, 1} as the
example in part b; is this a coincidence?

The expansions 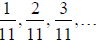are not all shifts of the same pattern, as was the case for
fractions with denominator 7. Why doesn’t the same method work in this case? Find
another fraction with prime denominator where 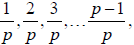are all shifts of the
same digits. What characterizes denominators with this property?

f. Notice that 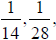and 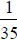all have repeating digits in their expansions that
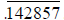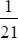are some shift of , but and 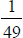have different digits (and the latter has period
42). Note also that 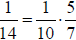and 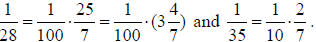Which
fractions of the form 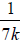will have repeating digits that are shifts of 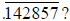Explain.

g. Now use the above to say something more general.