Get it on Google Play Get it on Apple Store

Math Camp Notes: Basic Proof Techniques

Basic notation:

• A => B . A implies B.

• A 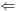B. B implies A. Note that A=> B does not imply B=> A. Example: If (A) a person eats two
hot dogs, she also (B) eats one hot dog. However, if (B) a person eats one hot dog, that does not
implie that she also (A) eats two hot dogs.

• A 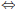B. A implies B and B implies A. Another way of saying this is that A holds if and only if (iff )
B holds, or that A is equivalent to B .

• ¬A. Not A, or the negation of A. Example: If A is the event that x ≤ 10, then ¬A is the event that
x > 10.

We seek for ways to prove that A=> B.

Direct Proofs

Deductive Reasoning

A direct proof by deductive reasoning is a sequence of accepted axioms or theorems such that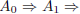
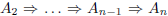, where 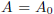and 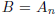. The difficulty is finding a sequence of theorems or
axioms to fill the gaps.

Example:

Prove the number three is an odd number.

Proof: Any number q is odd if there exists an integer m such that q = 2m+1. Let m = 1. Then three is an
odd number.

Contrapositive

A contrapositive proof is just a direct proof of the negation. If we want to prove that A => B, then we can
prove that ¬B => ¬A. For example, if (A) all people with driver's licenses are (B) at least 16 years old, then
if you are not (¬B) 16 years old, then you do not (¬A) have a driver's license. Or at least we hope .

Example:

Prove that is xy > 9, then either x > 3 or y > 3.
Proof: Suppose that both x ≤ 3 and y ≤3. Then xy ≤9.
 
Indirect Proofs

Contradiction

Suppose that we are trying to prove a proposition A, and we cannot prove it directly. However, we can
show that all other alternatives to A are impossible. Then we have indirectly proved that A must be true.
Therefore, the we can prove A => B by first assuming that 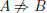and finding a contradiction.

In other words, we start o by assuming that A is true but B is not. If this leads to a contradiction, then
either B was actually true all along, or A was actually false. But since we assume A is true, then it must be
that B is true, and we have a proof by contradiction.

Example: Prove that 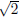is an irrational number.

Proof: Suppose not. Then 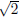is a rational number , so it can be expressed in the form 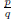, where p and q are
integers which are not both even. This implies that

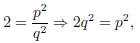
which implies that p2 is even, which in turn implies that q2 is not even. The fact that p2 is even also implies
that p is even, so there exists a integer m such that 2m = p. This implies



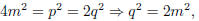
which means that q is even, a contradiction.

Induction

Induction can only be used for propositions about integers or indexed by integers. Consider a list of state-
ments indexed by the integers. Call the first statement P(1), the second P(2), and the nth statement P(n).
If we can prove the following two statements about the sequence, then every statement in the entire sequence
must be true:

1. P(1) is true.

2. If P(k) is true, then P(k + 1) is true.

Induction works because by 1., P(1) is true. By 2., P(2) is true since P(1) is true. Then P(3) is true by 2.
again, and so is P(4) and P(5) and P(6), until we show that all the P's are true. Notice that the number
of propositions need not be finite.

Example:

Prove that the sum of the first n natural numbers is .

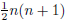Proof: Let n = 1. Then 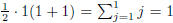. Now let n = k, and assume that .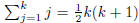
We add k + 1 to both sides to get



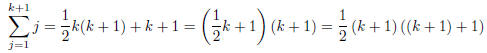
Proof Notation

It is common to use mathematical symbols for words while writing proofs in order to write faster. The
following are commonly used symbols :

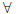For all, for any

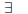There exists

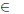Is contained in, includes as an element

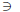Such that, is contained in (other way)

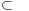Is a subset of

Homework

Prove the following by direct proof.

1. n(n + 1) is an even number.

2. The sum of the first n natural numbers is .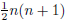

3. If 6x + 9y = 101, then either x or y is not an integer.

Prove the following by contrapositive.

1. n(n + 1) is an even number.

2. If x + y > 100, then either x > 50 or y > 50.

Prove the following by contradiction.

1. n(n + 1) is an even number.

2. 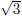is an irrational number.

3. There are in finitely many prime numbers.

Prove the following by induction.

1. n(n + 1) is an even number.

2. 2n ≤ 2n.

3. .

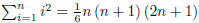4. The sum of the first n odd integers is n2 (This is the first known proof by mathematical induction,
attributed to Francesco Maurolico. Just in case you were interested.)

Find the error in the following argument, supposedly by induction:

If there is only one horse, then all the horses are of the same color. Now suppose that within any set of n
horses, they are all of the same color. Now look at any set of n+1 horses. Number them 1, 2, 3, . . . , n, n+1.
Consider the sets {1, 2, 3, . . . , n} and {2, 3, 4, . . . , n + 1}. Each set is a set of n horses, therefore they are all
of the same color. But these sets overlap, therefore all horses are the same color.

In first semester micro you will be introduced to preference relations . We say that 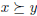, (read x is weakly
preferred to y ) if x is at least as good as y to the agent. From this, we can derive two important relations:

• The strict preference relation , 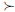, defined by but not 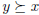. The strict preference
relation is read x is strictly preferred to y .

• The indifference relation, ~ , defined by 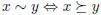and 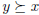. The indifference relation is read x
is indifferent to y .

We say that a preference relation is rational if :

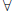• x, y, eithe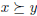r or .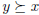

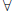• x, y, z, if 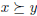and 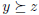, then .

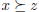Prove the following two statements given that preferences are rational:

1. If 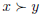and 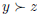, then .

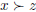2. If x ~ y and y ~ z, then x ~ z.

Prev Next