Math Review Lecture 2
Lecture 2: Algebra Basics
Algebra Basics
• Terminology
◦ A term is a numerical constant or the product (or
quotient) of a numerical constant and one or more
variables. Examples of terms are 2x and 3x
◦ An algebraic expression is a combination of one or
more terms. Terms in an expression are separated by
either + or – signs.
◦ In the term 3xy, the numerical constant 3 is called a
coefficient. In a simple term such as z, 1 is the
coefficient. A number without any variables is called a
constant term. An expression with one term, such as
3xy, is called a monomial; one with two terms , such as
4a + 2d, is a binomial; one with three terms, such as
xy + z – a, is a trinomial . The general name for
expressions with more than one term is polynomial.
Slide 3/38
• Operations with Polynomials
◦ All of the laws of arithmetic operations, such as the
associative, distributive, and commutative laws, are also
applicable to polynomials.
◦ All of the laws of arithmetic operations, such as the
associative, distributive, and commutative laws, are also
applicable to polynomials.
◦ Commutative law: a + b = b + a
◦ Associative law: (x + y) + z = x + (y + z)
◦ Distributive law: 2 (a +5) = 2a + 2(5) = 2a + 10
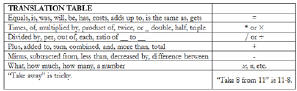
• Translating English Into Algebra: In some
word problems, especially those involving
variables, the best approach is to translate
directly from an English sentence into an
algebraic “sentence,” i.e., into an equation. The
table below lists some common English words
and phrases, and the corresponding algebraic
symbols .
Example: Steve is now five times as old as Craig was 5 years
ago. If the sum of Craig’s and Steve’s ages is 35, in how many
years will Steve be twice as old as Craig?
Lecture 2: Orders of Operation
Order of Operations
• PEMDAS: “Please Excuse My Dear Aunt Sally.”
Parentheses, exponents, multiplication, division,
addition, subtraction.
◦ Start with the innermost set of parentheses and work
outwards.
◦ Absolute value indicators are treated as parentheses.
◦ Multiplication & division are interchangeable
◦ Addition & subtraction are interchangeable
Lecture 2: Equations
Equations
• Equations: An equation is an algebraic sentence
that says that two expressions are equal to each
other. The two expressions consist of numbers,
variables, and arithmetic operations to be
performed on these numbers and variables.
• A linear or first -degree equation is an
equation in which all the variables are raised to
the first power. (There are no squares or cubes .)
n + 6 = 10
• A quadratic or second-degree equation
contains a squared term and no greater power.
The equation can be written as:
ax2 + bx + c = 0
where a is not equal to zero .
Lecture 2: Variation
Variation
• Direct Variation: One variable increases when
the other increases, and decreases when the
other decreases. For instance, the amount of
paint needed to paint a wall varies directly with
the area of the wall. When two quantities x and y
vary directly, their relationship can be expressed
by the equation y = kx, where k is a constant.
• Inverse Variation: In inverse variation, one
variable decreases when the other increases, and
increases when the other decreases. When two
quantities x and y vary inversely, their
relationship can be expressed by xy = k, or y =
k/x. One inverse relationship is rate × time =
distance. To cover a constant distance in less
time (decreasing time), you must go faster
(increasing rate).
Lecture 2: Functions
Functions
• Definition of a function:
A function is a rule
that assigns each element in the domain to one
and only one element in the range.
• The domain is the set of all possible numbers
that can be used as an input. This is also called
the explanatory or independent variable.
• The range is the set of all possible values that
are the output. This is also known as the
response variable or dependent variable.
• Functional Notation: y = f(x) = mx + b
• The domain is x and the range is f(x)
• For public policy applications, we must consider
the practical as well as mathematical meaning.
For example, it might not make sense to have a
negative quantity of books or a negative price.
Lecture 2: Correlation vs. Causation
• Correlation: Variables vary together, either
directly or inversely.
o Examples:
o A person’s height and weight
o Extent of fire damage and number of firefighters
• Causation: an event B always occurs when A
occurs (deterministic); the occurrence of A
increases the probability of B (probabilistic)
o Examples:
o Rain and a wet roof
o Air pollution and respiratory illness
Lecture 2: Solving Equations
Solving Equations
• The goal is to isolate the variable you’re solving
for on one side.
• What you do to one side, e.g. subtracting x, you
must always do to the other side.
• Add terms together, but only if they have the
same exponent. This process is known as
collecting like terms .
• Follow the order of operations.
• Adding and Subtracting Monomials: To
combine terms with the same variable and
exponent, keep the variable part unchanged
while adding or subtracting the coefficients.
o Examples:
2a + 3a =
10x – 2x =
• Adding and Subtracting Polynomials: Again,
combine like terms, where the exponent is equal.
o Example:
(3x2 + 5x – 7) – x2 =
• Remove parenthesis by distributing the
coefficient, as in 3(2y – 4) = 6y – 12
• Divide both sides by the coefficient to get
the variable by itself.
• Eliminate fractions by multiplying both sides
by the lowest common denominator . Or, if two
fractions are equal to each other, cross
multiply. This is a shortcut in which you simply
go from to

• Example of an equation with fractional
coefficients:
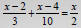
• Solve by multiplying both sides by the LCD ,
which is 30. Then distribute and rearrange.
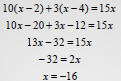
• Substitute known quantities in an expression
◦ Example: If x=2, replace x with 2 wherever x appears
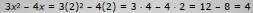
◦ Example: Suppose a person’s salary (S) is influenced
both by her years of education (E) and her
parents’ income(I):
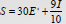
◦ Jason has a high school diploma; his parents’ average
salary was $80,000. Rachel has an MPA; her parents
earned $55,000. Who has the greater earning potential?
| Prev | Next |