Mathematics Cheat Sheet for Population Biology
1 Introduction
If you fake it long enough, there comes a point where you aren’t faking it any
more. Here are
some tips to help you along the way...
2 Calculus
Derivative The definition of a derivative is as follows. For some function f(x),
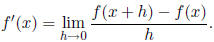
2.1 Differentiation Rules
It is useful to remember the following rules for differentiation . Let f(x) and
g(x) be two functions
2.1.1 Linearity
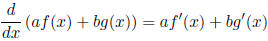
for constants a and b.
2.1.2 Product rule
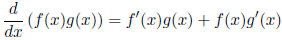
2.1.3 Chain rule
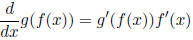
2.1.4 Quotient Rule
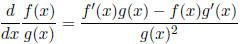
2.1.5 Some Basic Derivatives
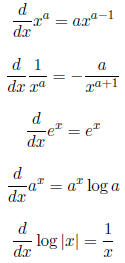
2.1.6 Convexity and Concavity
It is very easy to get confused about the convexity and concavity of a function.
The technical
mathematical definition is actually somewhat at odds with the colloquial usage.
Let f(x) be a
twice differentiable function in an interval I. Then:
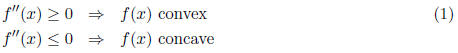
If you think about a profit function as a function of
time, a convex function would show
increasing marginal returns, while a concave function would show decreasing
marginal returns.
This leads into an important theorem (particularly for stochastic demography),
known as
Jensen’ s Inequality . For a convex function f(x),
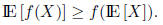
2.2 Taylor Series
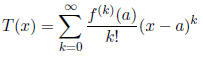
where 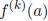 denotes the kth
derivative of f evaluated at a, and k! = k(k − 1)(k − 2) . . . (1).
denotes the kth
derivative of f evaluated at a, and k! = k(k − 1)(k − 2) . . . (1).
For example, we can approximate er at a = 0:
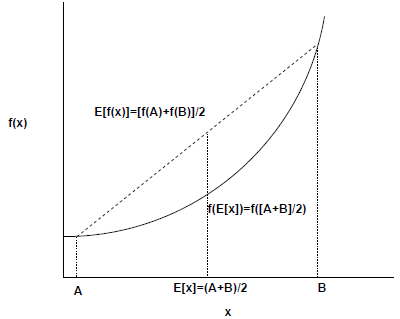
Figure 1: Illustration of Jensen’ s Inequality .
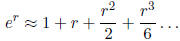
Expanding log (1 + x) around a = 0 yields:
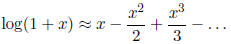
2.3 Jacobian
For a system of equations , F(x) and G(λ), the Jacobian matrix is
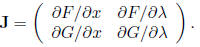
This is very important for the analysis of stability of
interacting models such as those for
epidemics and predator- prey systems . The equilibrium of a system is stable if
and only if the
real parts of all the eigenvalues of J are negative.
2.4 Integration
Linearity
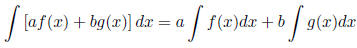
Integration by Parts
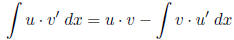
Some Useful Facts About Integrals
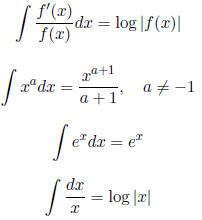
2.5 Definite Integrals
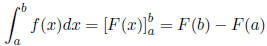
2.5.1 Expectation
For a continuous random variable X with probability density function f(x), the
expected value,
or mean, is
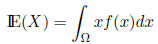
where the integral is taken over the set of all possible
outcomes Ω.
For example, the average age of mothers of newborns in a stable population:
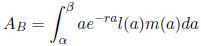
Since (from the Euler-Lotka equation) the probability that
a mother will be a years old in a
stable population is 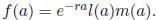
Some Properties of Expectation
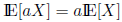
For two discrete random variables, X and Y ,
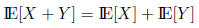
2.5.2 Variance
For a continuous random variable X with probability density function f(x) and
expected value
μ, the variance is
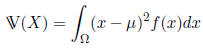
A useful formula for calculating variances:
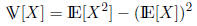
| Prev | Next |