Matrix Operations
Matrix Notation:
Two ways to denote m ·n matrix A:
In terms of the columns of A:
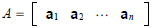
In terms of the entries of A:
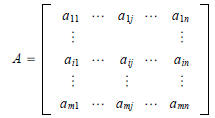
Main diagonal entries:___________________
Zero matrix :

THEOREM 1
Let A, B, and C be matrices of the same size, and let r and s
be scalars. Then
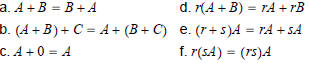
Matrix Multiplication
Multiplying B and x transforms x into the vector Bx. In turn, if we
multiply A and Bx, we transform Bx into 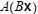 . So
. So
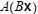 is the
is the
composition of two mappings .
Define the product AB so that 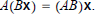
Suppose A is m ·n and B is n ·p where
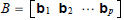 and
and
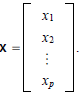
Then
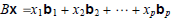
and
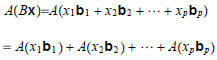
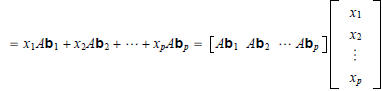
Therefore,
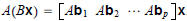
and by defining
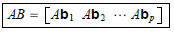
we have
![]()
EXAMPLE: Compute AB where
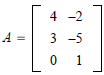 and
and
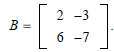
Solution :
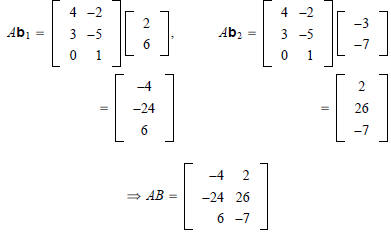
Note that Ab1 is a linear combination of the columns of A
and
Ab2 is a linear combination of the columns of A.
| Each column of AB is a linear combination of the
columns of A using weights from the corresponding columns of B. |
EXAMPLE: If A is 4 ·3 and B is 3 ·2, then what are the sizes
of
AB and BA?
Solution:
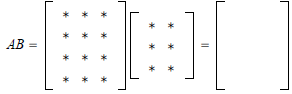
BA would be 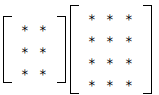
which is __________________.
| If A is m ·n and B is n ·p, then AB is m· p. |
Row-Column Rule for Computing AB (alternate method)
The definition
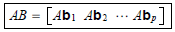
is good for theoretical work.
When A and B have small sizes, the following method is more
efficient when working by hand.
If AB is defined, let 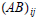 denote the entry in the ith row and jth
denote the entry in the ith row and jth
column of AB. Then
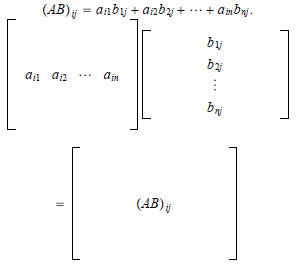
EXAMPLE 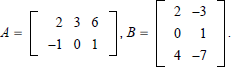 Compute
Compute
AB, if it is defined.
Solution: Since A is 2· 3 and B is 3 ·2, then AB is defined and
AB is _____× _____.
THEOREM 2
Let A be m ·n and let B and C have sizes for which the
indicated sums and products are defined.
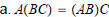 |
(associative law of multiplication ) |
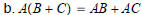 |
(left - distributive law ) |
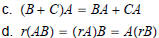 for any scalar r |
(right- distributive law ) |
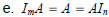 |
(identity for matrix multiplication) |
WARNINGS
Properties above are analogous to properties of real numbers .
But NOT ALL real number properties correspond to matrix
properties .
1. It is not the case that AB always equal BA. (see Example 7,
page 114)
2. Even if AB =AC, then B may not equal C. (see Exercise 10,
page 116)
3. It is possible for AB =0 even if A≠ 0 and B ≠0. (see
Exercise 12, page 116)
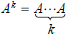
EXAMPLE:
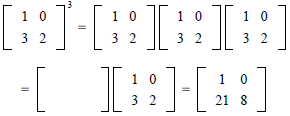
If A is m ·n, the transpose of A is the n · m matrix,
denoted by
AT, whose columns are formed from the corresponding rows of
A.
EXAMPLE:
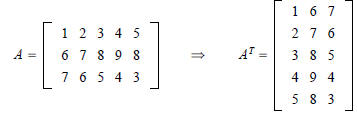
EXAMPLE: Let 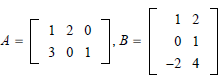 Compute
Compute
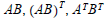 and
and 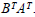
Solution:
THEOREM 3
Let A and B denote matrices whose sizes are appropriate for
the following sums and products.
a. 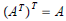 (I.e., the transpose of AT is A
(I.e., the transpose of AT is A
b. 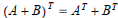
c. For any scalar r, 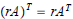
d. 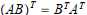 (I.e. the transpose of a product of matrices
(I.e. the transpose of a product of matrices
equals the product of their transposes in reverse order . )
EXAMPLE: Prove that 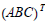 =_________.
=_________.
Solution: By Theorem 3d,
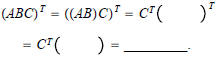
| Prev | Next |