Number Theory and Cryptography

Introduction.

Since the theory of numbers concerns itself with the familiar numbers 1, 2, 3, . . . , it might
seem at first glance to be little more than grade school arithmetic. We shall see that this is
far from true. The first clue that we are dealing with something more than a simple subject
is the three dots in the expression "1, 2, 3, . . . " The three dots, which translate into \and
so on" is the clue that tells us that we are dealing with infinitely many numbers. As such,
since we cannot examine all of the integers one by one, we may well expect to find many
mysteries and unsolved problems regarding these numbers. In fact this is true, as we shall
point out. However, we shall also be able to solve many problems that seem at first sight to
be intractable.

Throughout the text, when we speak of numbers, we understand ordinary whole numbers,
including zero and negative numbers. These are called integers. Much of what many students
know about numbers has been handed down as fact, and these are by now taken for granted.
In what follows, we shall investigate many of these \facts" a little more deeply. In many
cases, we will explain why they are true by giving proofs. Along the way, however, many new
ideas will be introduced. We should mention at the outset, that the topic of number theory
was once considered to be a field of mathematics with no practical applications. Recently,
however, it has proved extremely useful in the study and applications of cryptography. In a
later chapter, we shall explore this further.

We shall take for granted that you are familiar with some simple facts about integers. These
include the following.

Arithmetic operations . For example 43 + 58 = 101, 21 × 65 = 1, 365, 31² = 961. These
are easily found on a calculator, which we assume you have. However, a calculator has
limitations , since it can usually accept at most nine or ten digits. So if you have to add
or multiply two 40 digit numbers, you would have to revert to the old grade school way
of computation without a calculator or else have a powerful computer program to do this
exactly. In all arithmetic calculations, the answer is always understood to be exact. So if you
use a calculator to find that 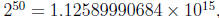you do not have the exact answer.
All you have is the first 12 digits of a 16 digit number. When dealing with integers, we will
usually want the exact answer. Calculators only give approximations for very large numbers.
For example, if you are used to writing 1/3 = .333, you are using an approximation. The
calculator which gives 1/3 = 0.333333333 is also giving an approximation.

Algebra. For example, you should know that (x+y)² = x²+2xy+y². and n(n+1) = n²+n,
and you should be able to solve the equation 2x+4 = 7x−3, and understand that the solution
need not be an integer.

For the present, we take it for granted that the reader of these notes knows what it means
for one number to divide another . We also take it for granted that the reader knows that
a prime number is a number larger than 1, which is divisible only by itself and by 1. A
few examples of numbers that are not primes (called composite numbers) are 51, 91, and
543,678,967,805. Do you see why? Here are a few questions about numbers. How many can
you answer?

• What is the 20th prime number?

• Is 571,435,871,001 prime number? What about 34,571?

• How many numbers divide 120?

• Is the fraction 28, 841=33, 043 in lowest terms ?

• The numbers 1− 1 + 41 = 41, 4 −2 + 41 = 43, 9 − 3+41 = 47, 16− 4+41 = 53 are
all primes. Is it true that n² − n + 41 is always a prime for all positive integers n?

• The numbers 4 = 2+2, 6 = 3+3, 8 = 5+3, and 10 = 7+3 are all sums of two primes.
Is every even number greatere than 2 a sum of two primes?

• The pairs (3,5), (5,7), (11,13), (17,19), (29,31) all consist of twin prime numbers.
(These are primes whose difference is 2.) Are there infinitely many twin primes?

• The odd perfect squares 1, 9, and 25 all leave a remainder of 1 when divided by 8. Is
this true for the square of every odd number?

• The numbers 2 = 1 + 1, 9 = 9+0, 13 = 4 + 9, and 34 = 9 + 25 are all sums of two
squares. However, 3, 14, and 21 are not. Which numbers are the sum of two squares?
Which are not?

• Which numbers are the sum of 4 squares?

The above list consists of a few questions in number theory. Though simple to ask, some are
questions, including two of the ones stated above, that nobody today still knows the answer
to. (These are the twin prime problem as well as the problem of the sum of two primes.) The
problem of factoring very large numbers turns out to be important in cryptography, where
the fastest computers still have to spend many hours deciding if a number is prime. We shall
analyze some of these problems in lecture and in lab to discover some of the methods used
to solve these and similar problems.

1 Division

Quotients and Remainders. We start by reviewing something probably learned in grade
school: how to divide two number to get a quotient and remainder. We will want to do this
on a calculator and on a computer. We first start with a simple example.

Example 1.1 Divide 57 by 13 and find the quotient and remainder.

Method:

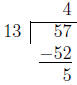
This is the way I did it in grade school. Since teaching methods change, you might not have
seen this before!

So the quotient is 4 and the remainder is 5.

The method is as follows. To divide 57 by 13, we estimate 4 as the approximate integer
quotient. Multiply 4 by 13 to get 52, subtract from 57 to get the remainder 5. Here, the
relationship of the quotient q and remainder r is

57 = 13 4 + 5 = 13q + r

Dividing this equation by 13, we obtain 57/13 = q + r/13, where r/13 is the fractional part
of the quotient 57/13. To do this with a calculator, we find 57/13 = 4:3846, and we can
read the quotient q = 4. The fractional part is .3846. As above, this is r/13, so we should
get the remainder r if we multiply by 13. If we do this on the calculator we get 4.9998. We
understand that this is only approximate, as most decimals are , and since we must have an
integer for the answer, we make the sensible guess that r = 5. The recommended (and safe)
way is to use whole numbers. Thus 57 = 13q + r and so r = 57 − 13q = 57 − 52 as before.

Let's illustrate with large numbers.

Example 1.2 Divide 68,934 by 5,791 and find the quotient q and remainder r. Express the
relationship between these numbers in a simple formula .

Method: Using a calculator, we find 68, 934/5, 791 = 11.9036. Therefore q = 11 and r =
68, 934 − 11(5, 791) = 5, 233. The relationship is 68, 934 = 5, 791(11) + 5, 233 = 5, 791q + r.
This computation can easily be set up on a spreadsheet. The lab for this course does this
on an Excel spreadsheet called Division. In theory this can done without a calculator or
computer, if you are willing to undergo a process called \long division." Happily we shall
not do this.

Summarizing: If a and b are integers with b > 0, we can always find a quotient q and a
remainder r such that

a = bq + r with 0 ≤ r < b (1)

Equation (1) is called the Division Algorithm. The quotient q is called a div b in most
computer languages. The remainder is called a mod b. The text introduced the \div" and
\mod" notations on page 67. The notation a div b is supposed to remind you that you
are dividing a by b but are conveniently dropping any remainder or fractional part. The
spreadsheet Excel does not have a div function, but it uses INT(a/b) instead. (Think: the
integer part of a/b.) In Excel, the remainder a mod b is written MOD(a, b).

Note that the remainder r is always less than the denominator b , and can be 0 (if the division
\comes out even.")

Definition 1.3 We say that b divides a, or that b is a factor of a, if a/b is an integer, or
equivalently that a = bq for some integer q. The standard way of writing this is b|a. (Read:
b divides a.) We also say that a is a multiple of b

Another way of putting this is that r = 0 in Equation (1).

In high school algebra, it was usually taken for granted that variables such as a, b, x, y des-
ignated real numbers. However, throughout this course we shall assume that they represent
integers, either positive, negative , or zero. This is an important change in usage. The word
number will similarly refer to integers only.

Such basic ideas as "even" and "odd" are de fined using the division algorithm. A number n
is even if 2|n, it is odd if 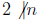(read as 2 does not divide n). Equivalently, a number is odd
if the remainder when divided by 2 is 1.

Do not confuse the "divides" sign | with the "divided by" sign /. Thus, we have 2|6, but
6/2 = 3.

The statement in (d) is called transitivity of division.

For example, if a number is divisible by 21 then it is divisible by 7. This follows from (d).
For suppose 21|n. Since 7| 21, we get 7|n by transitivity.

The following result is useful and fairly easy to prove.