Optimization

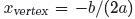Example 5. Use the formula to find the x- coordinate of the
vertex of the parabola represented by the quadratic function in Example 2.

In Example 2, the quadratic function was represented by the equation

f(x) = 2x² + 12x + 12.

In vertex form

f(x) = 2(x + 3)² − 6,

the coordinates of the vertex were easily seen to be (−3,−6) (see Figure 2). Let’s see
what the new formula for the x -coordinate of the vertex reveals.

As usual, compare f (x) = 2x² + 12x + 12 with f(x) = ax² + bx + c and note that
a = 2, b = 12 and c = 12. Thus, the x-coordinate of the vertex is given by
 

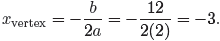
Note that this agrees with the previous result (see Figure 2). We could find the
y-coordinate of the vertex with

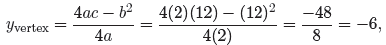
but we find this formula for the y-coordinate of the vertex a bit hard to memorize.
We find it easier to do the following. Since we know the x-coordinate of the vertex is
x = −3, we can find the y-coordinate of the vertex by simply substituting x = −3 in
the equation of the parabola . That is, with f(x) = 2x² + 12x − 12,

f(−3) = 2(−3)² + 12(−3) + 12 = −6.

Let’s highlight this last technique.

Finding the y-coordinate of the Vertex. Given the parabola represented by
the quadratic function

f(x) = ax² + bx + c,

we’ve seen that the x-coordinate of the vertex is given by x = −b/(2a). To find
the y-coordinate of the vertex, it is probably easiest to evaluate the function at
x = −b/(2a). That is, the y-coordinate of the vertex is given by

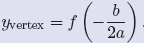
Let’s look at another example.

Example 6. Consider the parabola having equation

f(x) = −2x² + 3x − 8.

Find the coordinates of the vertex.

First, use the new formula to find the x-coordinate of the vertex.

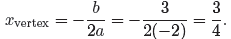
Next, substitute x = 3/4 to find the corresponding y-coordinate.

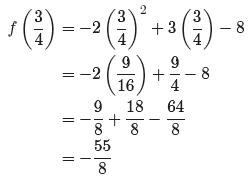
Thus, the coordinates of the vertex are (3/4,−55/8).

Applications

We’re now in a position to do some applications of optimization. Let’s start with an
easy example.

Example 7. Find two real numbers x and y that sum to 50 and that have a
product that is a maximum .

Before we apply the theory of the previous examples, let’s just play with the numbers
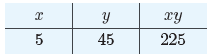
a bit to get a feel for what we are being asked to do. We need to find two numbers that
sum to 50, so let’s start with x = 5 and y = 45. Clearly, the sum of these two numbers
is 50. On the other hand, their product is xy = (5)(45) = 225. Let’s place this result
in a table.

For a second guess, select x = 10 and y = 40. The sum of these two numbers is 50
and their product is xy = 400. For a third guess, select x = 20 and y = 30. The sum
of these two numbers is 50 and their product is xy = 600. Let’s add these results to
our table.

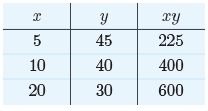
Thus far, the best pair is x = 20 and y = 30, because their product is the maximum
in the table above. But is there another pair with a larger product? Remember our
goal is to find a pair with a product that is a maximum. That is, our pair must have a
product larger than any other pair. Can you find a pair that has a product larger than
600?

Now that we have a feel for what we are being asked to do (find two numbers that
sum to 50 and that have a product that is a maximum), let’s try an approach that is
more abstract than the “guess and check” approach of our tables. Our first constraint is
the fact that the sum of the numbers x and y must be 50. We can model this constraint
with the equation

x + y = 50. (8)

We’re being asked to maximize the product. Thus, you want to find a formula for the
product. Let’s let P represent the product of x and y and write

P = xy. (9)

Note that P is a function of two variables x and y. However, all of our functions in
this course have thus far been a function of a single variable. So, how can we get rid
of one of the variables? Simple, first solve equation (8) for y.

x + y = 50
y = 50 − x  (10)

Now, substitute equation (10) into the product in equation (9).

P = x(50 − x),

or, equivalently ,

P = −x² + 50x. (11)

Note that P is now a function of a single variable x. Note further that the function
defined by equation (11) is quadratic. If we compare P = −x²+50x with the general
form P = ax² + bx + c, note that a = −1 and b = 50 (we have no need of the fact that
c = 0). Therefore, if we plot P versus x, the graph is a parabola that opens downward
(see Figure 3) and the maximum value of P will occur at the vertex. The x-coordinate
of the vertex is found with

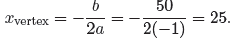
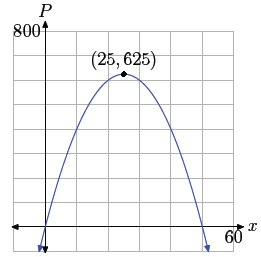
Figure 3. The maximum product
P=625 occurs at the vertex of the
parabola, (25, 625).

Thus, our first number is x = 25. We can find the second number y by substituting
x = 25 in equation (10).

y = 50 − x = 50 − 25 = 25.

Note that the sum of x and y is x+y = 25+25 = 50. There are two ways that we can
find their product. Since we now know the numbers x and y, we can multiply to find
P = xy = (25)(25) = 625. Alternatively, we could substitute x = 25 in equation (11)
to get

P = −x² + 50x = −(25)² + 50(25) = −625 + 1250 = 625.

When you compare this result with our experimental tables, things come together.
We’ve found two numbers x and y that sum to 50 with a product that is a maximum.
No other numbers that sum to 50 have a larger product.

Our little formula 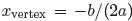has proven to be a powerful ally . Let’s try
another example.