Pre-calculus Algebra and Analytic Geometry
Reading Assignments
Section 1.5
Lesson Objectives
Note: This is a good time to become familiar with the layout of the
textbook. Each new section in the text
has introductory material that the student should read very carefully. You will
notice that the important
words or topics will be in boldface. For example, on page 44 the words
equivalent equations appear in
bold type and are defined as two equations with exactly the same solution. You
should be certain that you
understand the meaning of all boldface words.
The items found in the blue boxes are another important
feature of this textbook. Concepts found in the
blue boxes are very important and should be written down by the student. For
example, on page 49 you
will find one of the most important formulas in all mathematics , the
Quadratic Formula .
| THE QUADRATIC FORMULA |
| The roots of the quadratic equation ax 2 + bx + c
= 0, where a ≠ 0, are
|
The examples are probably the most important aspect of
each section. Each section contains several
worked examples that are very similar to your homework problems. You should work
through the
examples very carefully and refer to them while doing your homework. Follow the
directions in the
lesson and then work odd- numbered practice problems related to the reading
material. All odd-numbered
problems have solutions in the back of the book.
Objectives for Section 1.5
• Know how to solve a linear equation ax + b = 0.
Example:
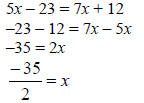
• Know that to solve an equation you can do the following:
1. Add or subtract the same quantity from both sides.
2. Multiply or divide both sides by the same nonzero quantity.
Note: The example 5x – 23 = 7x + 12, given above, uses both 1 and 2.
3. Raise both sides of an equation to the same power . Examples are given on the
next page.
• Know the definition of the Quadratic Equation.
ax2 + bx + c = 0, where a, b, and c are real and a ≠ 0
• Know the Zero -Product Property.
• Be able to factor a quadratic or trinomial expression or equation . (See
Section 1.3, pages 27–31, for a
review of factoring.)
Examples:
x2 – 3x – 28 = (x – 7)(x + 4)
6x2 + x – 12 = (2x + 3)(3x – 4)
• Be able to solve a simple quadratic equation by extracting square roots .
Note: You should use this method when b = 0.
Example:
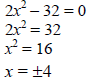
• Be able to solve a quadratic equation by completing the
square.
Example:
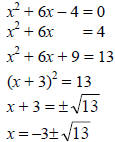 |
|
| Add 4 to both sides. | |
Add
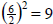 to both sides. to both sides. |
|
| Factor. | |
| Take square roots of both sides. | |
| Subtract 3 from both sides. |
• Know the Quadratic Formula and how to use it.
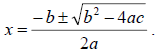
• Be able to determine the types of solutions of a
quadratic equation by checking the discriminant
b2 – 4ac.
1. If b2 – 4ac > 0, then there are two distinct real solutions.
Example:
16x2 + 8x – 3 = 0
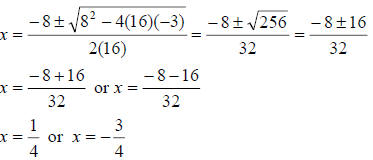
2. If b2 – 4ac = 0, then there is exactly one real
solution.
Example:
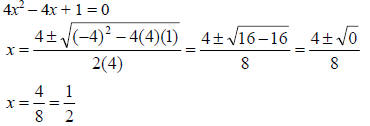
3. If b2 – 4ac < 0, then there are no real solutions.
Example:
| Prev | Next |