Rational Numbers

1 Addition and Subtraction

We have now established what a fraction is and how we tell when two fractions are going
to be equal, even how we think of the natural numbers as fractions. At this point we need
to know how to add and subtract them . The rules for adding and subtracting fractions are
simply the following .

Definition 4 (Adding Fractions). The rule for adding fractions is:

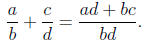
Definition 5 (Subtracting Fractions). The rule for subtracting fractions is:

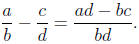
There is a theme running from determining if two fractions are equal and adding/subtracting
fractions: : :cross multiplication. In both cases, the numerators are still just cross multiplied
and put together with the respective operations and the denominators are multiplied . After
the operation is performed, the fractions are then simplified so that the numerator and denominator
have no factors in common, that is they are relatively prime. Remember, we
have even discussed a way to calculate the GCD of two numbers in a reasonably fast way,
the Euclidean Algorithm.

Example 4. Perform the operation.

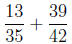
Solution . We simply cross multiply and add for the numerator and multiply the denominator

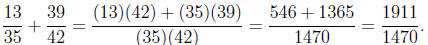
Now this fraction would be very difficult to factor the numerator and denominator in order
to simplify, but we can get the GCD with the Euclidean Algorithm.

1911 = (1)(1470) + 441
1470 = (3)(441) + 147
441 = (3)(147) + 0

Therefore, the GCD of the numerator and denominator is 147. Thus, we can write

1911 = (147)(13) and 1470 = (147)(10).

Then simplifying our fractions is just

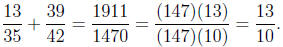
Note. The only tool which I used in computing the addition in the example was a simple
pocket calculator which did not do fractions, but only used it for the multiplication in
the cross multiplication and in determining the quotients and remainders in the Euclidean
Algorithm!

That was fun …so let's do it again!

Example 5. Peform the following operation.

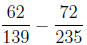
Solution. Again, we just cross multiply and subtract in the numerator and multiply the
denominator.

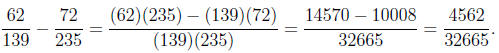
Now we apply the Euclidean Algorithm to simplify it.

32665 = (7)(4562) + 731
4562 = (6)(731) + 176
731 = (4)(176) + 27
176 = (6)(27) + 14
27 = (1)(14) + 13
14 = (1)(13) + 1
13 = (13)(1) + 0

Thus, our GCD will be 1 and we have no common factor in the numerator and denominator
and our fraction is already simplified. As our final answer, we have

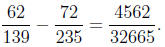
Now think about what you have learned before about adding with fractions. At no
time did I look at decimal expansions of anything. Not once did I talk about nding the
least common denominator, converting the fractions and then performing the operation and
simplifying the result. Nothing was used for the \hard to deal with" operations on fractions
but the simple rules for putting them together and the Euclidean Algorithm for simplifying
them. Absolutely amazing!

Now that we have seen this method of adding fractions and simplifying them, let us
see how the more \traditional" methods of dealing with fractions t in to all of this. Even
according to our text, pp 25-26,

To add (or subtract) fractions with unlike denominators, we must rst rewrite
each fraction with the same, or a common denominator. The smallest number
that is divisible by two or more denominators is called the least common
denominator or LCD.

There is absolutely nothing wrong with adding fractions this way. Remember that in converting
to equivalent fractions , we have to multiply the numerator and denominator by a
common factor. First lets see what happens when we add fractions with the same denominator
with our formula above .

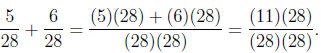
Note. If you are wondering how I came up with the (11)(28) in the numerator without
multiplying it was nothing more than the 5 and the 6 added together. When we have 5 of
something and add 6 of something, we end up with 11 of the something. In this case the
something was just 28.

You can see that we have a factor of 28 in the numerator and denominator, so our result
will be equal to

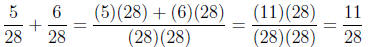
which is what we would get if we simply added straight across.

Exercise. Make up your own fractions with the same denominator and add them and subtract
them to convince yourself that you always have a common factor of the original denominator
to simplfy after you use our addition formula.

Now as for this business of finding a common denominator. Guess what, we can use
the Euclidean Algorithm and trick that works because of prime factorization and the Fundamental
Theorem of Arithmetic to get our least common denominators too! Man, that
Fundamental Theorem of Arithemetic is useful!

Let us take our examples above and do the problems the way the book would like.

Example 6. Perform the operation.

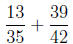
Solution. In order to find the LCD of the two denominators we can first find the GCD of
them : : : hello Euclidean Algorithm again! Here we go,

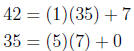
and our GCD is 7. Now for finding the LCD, here is the trick.

Therefore, our LCD is going to be

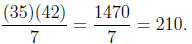
In order to convert the fractions we need to know how many times each denominator goes
into 210.

210 = (35)(6) and 210 = (42)(5):

Therefore, in converting our fractions, we have

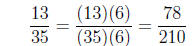
and

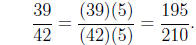
Therefore, in doing the operation, we have

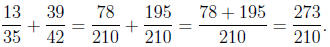
Now as a last step, we simplify the fraction with the Euclidean Algorithm.

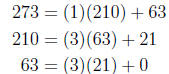
Thus, we have a common factor of 21 in the numerator and denominator with

273 = (21)(13) and 210 = (21)(10):

As our last step we have ,

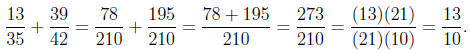
Of the two ways to do it, which one seems like more work ? Does that mean that we should
abandon the method of finding LCD and converting the fractions all together? Absolutely
not! Like all tools, there is a time and place to use them and only experience in doing
fractions will let you know which is best to try. One instance when it might be easier to
use the LCD method is when the denominators are different , but both are a power of the
same number. Here is a problem anyone doing home repair around the house might have
encountered.

Example 7. Perform the operation.

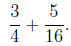
Solution. Both denominators are powers of 2 and show up on any English ruler or measuring
tape you might have. In this case, cross multiplying and adding make the numbers get bigger
than we would like to handle in our head, so we take the LCD approach and notice that 4
goes into 16, hence the LCD is 16. Converting, we have

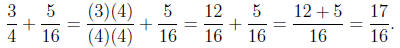
References